Theory of Thermoluminescence
by Dr. Reuven Chen
Raymond and Beverly Sackler School of Physics and Astronomy, Tel Aviv University, Tel Aviv 69978, Israel.
The basic theory of thermoluminesence (TL) is based on the occurrence of imperfections, impurities, and defects, found within an insulating material. These lattice sites may capture electrons and holes during the excitation of the sample and later, during the heating, these charge carriers can recombine and produce the emission of light in the form of a TL glow curve. The process leading to recombination includes, in many cases, the transition of charge carriers through the conduction or valence band, but localized transitions may also take place. In most cases, the theory consists of solving the relevant sets of coupled differential equations,either by using some simplifying assumptions or by solving numerically the equations for certain sets of trapping parameters.
Contents
1 Introduction
The effect of thermoluminescence (TL) is the emission of light from solids, usually crystalline insulators, following excitation, usually by some irradiation. Energy is absorbed in the sample during the excitation, and released during the heating, yielding a glow curve, namely, a graph of emitted-light intensity versus temperature. The glow curve usually includes one or more glow peaks that may be either separate or overlapping. The emitted light may include different spectral components which indicate different transitions taking place during the heating. Practically always, the glow curve can be detected only following a first heating, and a subsequent heating does not produce any light emission until another irradiation takes place. The main application of TL, along with the closely related effect of optically stimulated luminescence (OSL) is in dosimetry. The dependence of the measured luminescence on the preceding excitation dose should be taken into consideration; linear dose dependence is desirable, but other dependencies often occur. Different dose-dependence behaviours are observed when using different sources of radiation. [math]\alpha[/math], [math] \beta [/math], and [math]\gamma[/math] irradiations as well as X-rays, UV light, high-energy particles and neutron beams may be used to induce TL in different crystals. Another application of TL, derived from the property of dose dependence is the dating of archaeological and geological samples. An important subject in the study of TL has to do with the evaluation of the trapping parameters, mainly the activation energy and the frequency factor of the involved traps. Also the stability of the TL signal at ambient temperature has been studied extensively. Normal thermal fading as well as anomalous fading have been observed in different materials and a number of theoretical explanations have been provided. TL has been studied in hundreds of different materials in the quest for an optimal material for TL dosimetry.
2 Basic Theory
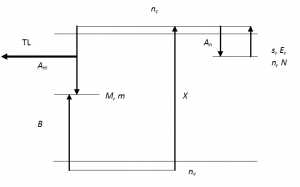
The main requirement for producing a glow peak is the occurrence of two imperfections in the lattice. During excitation, one is capable of trapping an electron and the other traps a hole. A schematic energy level diagram is shown in Fig. 1. The basic theory of TL was first introduced by Randall and Wilkins (1945). These authors assumed that during excitation by irradiation, electrons are trapped in an electron trap of concentration N (cm[math]^{-3}[/math]), and holes are trapped in hole centres, M (cm[math]^{-3}[/math]). During heating, electrons are raised thermally into the conduction band and, according to this basic theory, they recombine almost immediately with a hole in a centre to produce photons. The basic differential equation for this process was given by Randall and Wilkins as a first-order equation
[math]I(T)=-\frac{dn}{dt}=sn\, exp\left ( -E/kT \right )\tag{1}[/math]
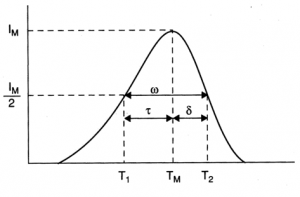
where n (cm[math]^{-3}[/math]) is the instantaneous concentration of trapped electrons, E (eV) the activation energy for releasing trapped electrons, s (s[math]^{-1}[/math]) the frequency factor, k (eV/K) Boltzmann's constant, T (K) the temperature, t (s) is the time and I the emitted intensity. As is, the units of I(T) are cm[math]^{-3}[/math]s[math]^{-1}[/math], however, a dimensional constant should be added which has been set arbitrarily to unity. With this constant, I(T) will be in units of photons per second or energy per second. In order to solve this equation, one should use a heating function that relates temperature and time. In many cases, a linear function is used, [math]T=T_{0}+\beta t[/math] where [math]\beta[/math] (K/s) is the constant heating rate and [math]T_{0}[/math] the initial temperature. The solution of Eq. (1) is [math]I(T)=n_{0}s\, exp\left ( -E/kT \right )\, exp\left [ -\frac{s}{\beta }\int_{T_{0}}^{T}exp\left ( -E/k\theta \right )d\theta \right ]\tag{2}[/math] where [math]n_{0}[/math] is the concentration of trapped electrons at the beginning of heating. This function represents an asymmetric peak with a slower increase and faster decrease. Figure 2 depicts schematically the TL intensity in a first-order TL peak. Here, [math]T_{m}[/math] is the maximum temperature and [math]T_{1}[/math] and [math]T_{2}[/math] are the low- and high-temperature half intensity temperatures, respectively. [math]\alpha[/math] and [math]\beta[/math] are the low- and high-temperature half peaks and [math]\omega[/math] is the full half peak. The symmetry of the peak is usually measured by the symmetry factor [math]\mu _{g}=\frac{\delta }{\omega }[/math] which for the first-order case is typically ~0.42 (see e.g. Chen and McKeever, 1997). The condition for the maximum of a first-order peak is reached by setting the derivative of Eq. (2) to zero which yields [math]\frac{\beta E}{kT_{m}^{2}}=s\, exp\left (-E/kT_{m} \right )\tag{3}[/math] In a more comprehensive approach, one should consider the possibility of retrapping of freed electrons from the conduction band into the original trap which has been described by Halperin and Braner (1960). The processes taking place during the heating of the sample, when one trap and one centre are involved, are shown in Fig. 1. The governing equations are
[math]I=-\frac{dm}{dt}=A_{m}mn_{c}\tag{4}[/math]
[math]-\frac{dn}{dt}=sn\, exp\left ( -E/kT \right )-n_{c}(N-n)A_{n}\tag{5}[/math]
[math]\frac{dn_{c}}{dt}=sn\, exp\left ( -E/kT \right )-n_{c}\left [ (mA_{m}+(N-n)A_{n} \right ]\tag{6}[/math]
where [math]A_{m}[/math] (cm[math]^{3}[/math]s[math]^{-1}[/math]) and A[math]_{n}[/math] (cm[math]^{3}[/math]s[math]^{-1}[/math]) are respectively the recombination- and retrapping-probability coefficients. Halperin and Braner (1960) made the well-known "quasi-equilibrium" assumptions, namely
[math]\left | \frac{dn_{c}}{dt} \right |\ll \left | \frac{dn}{dt} \right |,\left | \frac{dm}{dt} \right |;\; n_{c}\ll n,m\tag{7}[/math]
and reached the simplified equation
[math]I=-\frac{dm}{dt}=sn\, exp\left ( -E/kT \right )\frac{A_{m}m}{A_{m}m+A_{n}(N-n)}\tag{8}[/math]
In the simple case where there is only one trap and one centre, n=m and Eq. (8) reduces to
[math]I=-\frac{dn}{dt}=sn\, exp\left ( -E/kT \right )\frac{A_{m}n}{A_{m}n+A_{n}(N-n)}\tag{9}[/math]
which is an equation with one unknown function, [math]n(t)[/math]. Further possibilities of simplifying Eq. (9) have to do with different relations between recombination and retrapping. If recombination dominates, [math]A_{m}m\gg A_{n}(N-n)[/math], then Eq. (9) reduces to the first-order case of Eq. (1). If, on the other hand, retrapping dominates [math]A_{m}m\ll A_ {n}(N-n)[/math], Eq. (9) reduces to
[math]I=-\frac{dn}{dt}=\frac{sA_{m}}{NA_{n}}n^{2}\, exp\left ( -E/kT \right )\tag{10}[/math]
which is a second-order TL equation. Alternatively, if one assumes (see e.g. Garlick and Gibson, 1948), equal probabilities for recombination and retrapping, [math]A_{m}=A_{n}[/math], one gets from Eq. (9)
[math]I=-\frac{dn}{dt}=\frac{s}{N}n^{2}\, exp\left ( -E/kT \right )\tag{11}[/math]
which is also a second-order equation. Since the trap and centre are two independent entities, the latter condition for second-order kinetics is less likely to occur than the former. Both equations (10) and (12) can be written in a combined way
[math]I=-\frac{dn}{dt}=s'exp\left ( -E/kT \right )n^{2}\tag{12}[/math]
where [math]s'[/math] is a "pre-exponential" factor with units of cm[math]^{3}[/math]s[math]^{-1}[/math]. The solution of Eqs. (10-12) is a peak-shaped curve which is nearly symmetric, with a typical shape factor [math]\mu _{g}\sim 0.52[/math]. Glow peaks with intermediate symmetries between that of first- and second-order have been observed, prompting May and Partridge (1964) to suggest the use of "general-order" kinetics, namely, using the equation
[math]I=-\frac{dn}{dt}=s'exp\left ( -E/kT \right )n^{b}\tag{13}[/math]
where [math]b[/math] is the order of the kinetics which may be between one and two. The solution of this equation is a peak-shaped curve with a symmetry factor between 0.42 and 0.52. It should be noted however that Eq. (13) is merely heuristic in the sense that it cannot be reached from the initial equations (4-6). Moreover, the units of the pre-exponential factor [math]s'[/math] in the general-order case are cm[math]^{3(b-1)}[/math]s[math]^{-1}[/math]. In the first- and second-order cases, this yields the known units of these factors but it does not have much physical meaning when [math]b\neq 1[/math] and [math]b\neq 2[/math].
An alternative way of presenting TL peaks with kinetics intermediate between first- and second-order has been suggested by Chen et al. (1981), namely, the "mixed-order kinetics" given by
[math]I=-\frac{dn}{dt}=s'n\left ( n+c \right )exp\left ( -E/kT \right )\tag{14}[/math]
where [math]c[/math] is a constant associated with the concentration of disconnected traps or centres and [math]s'[/math] is a pre-exponential factor with units of cm[math]^{3}[/math]s[math]^{-1}[/math] like in the second-order case. Obviously, [math]c\gg n[/math] results in the first-order equation and [math]c\ll n[/math] leads to the second-order case. Of course, different intermediate cases are possible.
3 Methods for Evaluating Trapping Parameters
A number of methods have been developed for evaluating the activation energy from the shape of the TL peak. The simplest one appears to be the "initial-rise" method. If we consider, for example, Eq. (1), at the low temperature end of the peak, n varies only slightly, and we can write
[math]I(T)\propto exp\left ( -E/kT \right )\tag{15}[/math]
Garlick and Gibson (1948) suggested to plot [math]\ln (I)[/math] as a function of [math]1/T[/math] in the low temperature range which should yield a straight line, the slope of which is [math]–E/k[/math]; from this, [math]E[/math] can be calculated. The method is considered to be generally applicable although some "pathological" examples have been reported in the literature. In all the instances described in Eqs. (8-14), as long as [math]n[/math] and [math]m[/math] vary only slightly in the initial-rise range, the described method is expected to yield an acceptable value for [math]E[/math]. The main problem here is that the initial-rise range is limited to, say, 5% of the maximum intensity and in low-intensity peaks this may be a significant restriction. Several methods have been developed based on various shape features of the TL peak. As an example, for a first-order peak one can use the formula
[math]E=2.52\frac{kT_{m}^{2}}{\omega }+2kT_{m}\tag{16}[/math]
where [math]\omega[/math] is the full width defined above. Extension of this formula to non-first-order peaks use interpolation on the symmetry factor [math]\mu_{g}[/math] (see e.g. p. 66 in Chen and Pagonis, 2011). Another group of methods involves the shift of the maximum temperature [math]T_{m}[/math] while changing the heating rate (see Hoogenstraaten, 1958). Equation (3) can be re-written as
[math]\beta =\left ( sk/E \right )T_{m}^{2}\, exp\left ( -E/kT_{m} \right )\tag{17}[/math]
Increasing the heating rate would necessarily result in an increase of the right-hand side of the equation. However, since the right-hand side is an always increasing function of [math]T_{m}[/math], this causes a shift upwards of [math]T_{m}[/math]. Hoogenstraaten (1958) suggested a method involving several heating rates. Considering Eq. (3), it can be seen that a plot of [math]\ln \left ( T_{_{m}}^{2}/\beta \right )[/math] versus [math](1/T_{m})[/math] should yield a straight line, from the slope of which, [math]E/k[/math], the activation energy E can be determined. Although this method has been shown here to be valid for the first-order situation, several works have demonstrated that this various heating rates method is rather general and can be used, e.g, for cases covered by the set of equations (4-6). Another method that has been used extensively is the curve-fitting method. Generally speaking, one compares the shape of the measured TL peak with a theoretical curve with the appropriate number of parameters. This can be done, for example, by minimizing the root-mean-squares deviations. If [math]I_{i}[/math] are the measured intensities and [math]I(T_{i})[/math] are the calculated intensities
[math]S=\left \{\sum_{i=1}^{N} \left [ I(T_{i})-I_{i} \right ]/N \right \}^{1/2}\tag{18}[/math]
Important extensions to the curve fitting are the methods of deconvolution. Quite often, TL is measured as a rather complex glow curve that includes several overlapping peaks. In particular, this is the case in the important dosimetric material LiF:Mg,Ti(TLD-100). Horowitz and Yossian (1995) have provided an extensive and detailed review of the subject in a review paper. One has to guess the number of the overlapping peaks in a given glow curve in order to perform the deconvolution. Either first-order or general-order kinetics must be assumed, and the deconvolution program minimizes the difference between the experimental and generated curves, thus yielding the trapping parameters of the individual peaks. It should be noted that some criticism of the deconvolution method has been expressed in the literature since the deconvolution method does not take into consideration the possible interaction between peaks due to trapping of electrons from one trap into deeper traps.
As pointed out, a single TL peak may be of first- or second-order and intermediate cases are possible. It could be expected that the same is true for the components of a glow curve with several separate or overlapping peaks. However, several researchers reported that in a series of peaks emitted from the same sample, first-order kinetics are prevalent (see e.g., Lewandowski and McKeever, 1991). Chen and Pagonis (2013) have shown, using analytical considerations as well as numerical-simulation results that even in cases of strong inter-peak trapping approximately first-order peaks can usually be expected for the peaks in a series except for the highest-temperature one which tends to have second-order features. This fact gives partial justification to the assumption made in some deconvolution programs which assume that the component peaks are of first order.
4 Dose Dependence of TL
The main applications of TL and the related phenomenon of optically stimulated luminescence (OSL) are in dosimetry and the method derived thereof of evaluating the ages of archaeological and geological samples. It is obvious that for the ease of evaluating the absorbed dose using an appropriate calibration, a linear dose dependence of the TL intensity on the relevant radiation is desirable. Unfortunately, linearity in broad ranges of dose is not very common. To begin with, in practically all cases, the dose dependence deviates from linearity at high doses, where saturation of the traps and/or centres is approached. Such sublinear dose dependence may occur following a range of linear dependence. Sometimes, it may take place even at the lowest doses. Another effect sometimes observed is the superlinear dose dependence of TL, which also may occur at the lowest doses or following a range of linear dependence. The mechanism for superlinear dose dependence of TL and OSL usually includes different kinds of competition. This includes competition that takes place during excitation and competition that occurs during heating. The first model of competition during the excitation stage was given by Bowman and Chen (1979) and considered the competition of electrons falling into the active trap and into a competing, usually deeper disconnected trap. Using a simple, intuitive explanation, at low doses, the excitation fills both traps linearly. At a certain dose, the competing trap saturates and therefore, more electrons are made available to the trap of interest. This causes fast though linear filling of the trap. However, the transition region from one linear range to the other would appear to be superlinear since the transition occurs continuously. Bowman and Chen wrote the relevant set of differential equations and reached an approximate expression that, with an appropriate choice of trapping parameters, yielded a dose-dependence curve which starts linearly, continues superlinearly and then tends to saturation.
As for thermoluminescence superlinearity that starts as of the lowest doses, Kristianpoller et al. (1971) explained it in terms of competition during heating (for more details see Chen and Pagonis, 2011, pp. 198-205). Without competition, one might expect the area S under a glow peak to be min([math]n_{0},m_{0}[/math]) where [math]n_{0}[/math] and [math]m_{0}[/math] are, respectively, the concentrations of electrons in traps and holes in centres following excitation, prior to the heating-stage readout. If [math]n_{0}[/math] and [math]m_{0}[/math] are linearly dependent on the dose of excitation, the measured TL intensity is also linear with the dose. Kristianpoller et al. (1971) showed that in the presence of a strong competing trap, the behaviour of the area under the curve is, due to competition during heating
[math]S\propto n_{0}m_{0}\tag{19}[/math]
and if [math]n_{0}\propto D[/math] and [math]m_{0}\propto D[/math], then [math]S\propto D^{2}[/math]. In a later work (see e.g. p. 202 in Chen and Pagonis, 2011),these two approaches were combined, using a numerical simulation involving a model with two competing traps and one recombination centre. In this case, TL intensity increased as a [math]D^{2}[/math] function or even faster, the main effect being related to competition during heating.
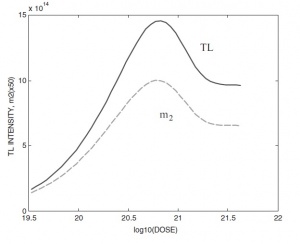
The TL intensity in different materials is usually a monotonically increasing function of the dose, which usually reaches a saturation value at high doses. In several materials, however, non-monotonic dose dependence has been observed. The TL intensity reached a maximum and then decreased at higher doses. For example, Yukihara et al. (2003) described a somewhat superlinear dependence up to ~10 Gy following [math]\beta[/math] irradiation of the 450K peak in Al[math]_{2}[/math]O[math]_{3}[/math]:C. The peak reached a maximum value and declined at higher doses. Chen et al. (2006) suggested a model which assumed the existence of two trapping states and two kinds of recombination centres. The competition over charge carriers during excitation and heating was examined using numerical simulations as well as intuitive considerations. The authors chose a set of physically significant trapping parameters and performed the simulation of the three stages of the relevant experiment, namely: excitation, relaxation and heating. The results show an increase of the TL maximum (solid line) with the dose up to a maximum at a dose of 7[math]\times [/math]10[math]^{20}[/math] m[math]^{-3}[/math], followed by a decrease of ~35% after which the maximum TL intensity tends to level off at higher doses. This behaviour is very similar to experimental results reported in some materials.
5 Dose-rate Dependence
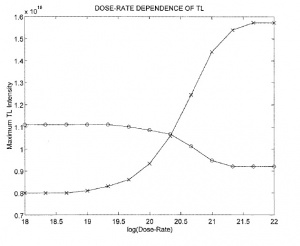
When the dose dependence of TL has been discussed, the implied assumption has been that the results are not changed if the dose is changed by altering the rate at which the dose is applied or by varying the length of time of excitation with a constant dose rate. It should be noted that the dose rate and the time of excitation are two independent variables and in some cases, the resulting luminescence may depend on the dose rate even when the total dose is unchanged. When geological and archaeological dating are concerned, the natural dose is usually as low as 3[math]\times[/math]10[math]^{-11}[/math]Gy/s whereas the laboratory dose rate applied for calibration may be as high as several Gy/s. We have to distinguish between a dose-rate effect which has to do with the thermal decay during excitation and the "genuine" dose-rate effect where the TL signal is stable such that no thermal decay is expected at ambient temperature. Groom et al. (1978) reported such an effect in quartz when no thermal decay takes place. A decrease by a factor of ~5 was observed with decreasing dose rate (and unchanged total dose)in powdered samples of Brazilian crystalline quartz with [math]^{60}[/math]Co [math]\gamma[/math]-irradiation at dose rates ranging from 1.4[math]\times[/math]10[math]^{-3}[/math] to 3.3 Gy/s. Valladas and Ferreira (1980) distinguished between three components of TL emission from quartz: UV, blue and green. Using the same total dose at two dose rates, three orders of magnitude apart, they found different behaviours of the three components. The UV component was nearly twice as large with the high dose rate as with the low one. In the green component, the low dose rate yielded about 10% less than in the high one. As for the blue component, the low dose rate yielded about 50% more TL than the high one. Chen and Leung (2000) gave a model with one trapping state and two kinds of recombination centres which partly simulated the situation described by Valladas and Ferreira (1980), namely, that two spectral components in quartz behave in opposite directions, one decreases and one increases with the dose rate. Chen and Leung wrote and solved the relevant sets of coupled differential equations for the three stages of excitation, relaxation and heating, and recorded the two emissions, [math]I_{1}=-dm_{1}/dt[/math] and [math]I_{2}=-dm_{2}/dt[/math], where [math]m_{1}[/math] and [math]m_{2}[/math] are the concentrations of the two recombination centres. Simulated dose-rate dependence results are given in Fig. 4.
6 Concentration Quenching
TL as well as other luminescence effects in solids are related to the existence of impurities and defects in the host material. It is usually expected that when a certain imperfection causes the appearance of TL, higher imperfection concentration would result in more emitted luminescence for a given excitation dose. A number of experiments have shown, however, that a non-monotonic dependence on the impurity concentration is possible. The response to irradiation increases with the impurity concentration up to a maximum, and then it declines with higher concentrations. This effect has been termed concentration quenching (CQ). The first concentration quenching of TL was reported by Medlin (1974) who described the dependence of a 350 K peak in calcite on the Mn[math]^{++}[/math] impurity content and showed that for a given irradiation, a maximum intensity was reached for a certain impurity concentration, followed by a decrease at higher impurity levels. Medlin also found the effect in Pb[math]^{++}[/math] doped calcite and reported that the maxima for two observed peaks occurred at different concentrations. Several more results of the same sort were found in various other materials with different impurities. Chen et al. (2011) proposed a model with three electron trapping states and one recombination centre. They wrote the appropriate set of simultaneous differential equations, chose a relevant set of trapping parameters and solved the equations in the usual sequence of excitation, relaxation and heating. This sequence was repeated for different concentrations of the recombination centre and the results showed a non-monotonic dependence of the two peaks associated with the two trapping states, similar to the experimental results of Medlin.
7 Conclusion
The basic theory of the main facets of thermoluminescence has briefly been discussed. It should be noted that the models discussed are limited to the cases where the whole sample is uniformly excited during the initial irradiation. This is the case where the absorption of the applied radiation is not very strong, otherwise there will be a gradient of excitation from the outer surface moving towards the center. Also, these models assume that during both excitation and read-out, charge carriers move between traps and centers via the conduction and valence bands. Localized transitions may also take place, but have not been considered here.
8 References
Bowman, S. G. E. and Chen, R. "Superlinear filling of traps in crystals due to competition during irradiation", J. Lumin. 18 (1979): 345-348.
Chen, R. Kristianpoller, N., Davidson, Z. and Visocekas, R. "Mixed first and second order kinetics in thermally stimulated processes," J. Lumin. 23 (1981): 293-303.
Chen, Reuven and McKeever, Stephen W. S.Theory of Thermoluminescence and Related Phenomena. Singapore: World Scientific Publishing, 1997.
Chen, R., Lo, D. and Lawless, J. L. "Non-monotonic dose dependence of thermoluminescence," Radiat. Prot. Dosim., 119 (2006): 33-36.
Chen, R. and Leung, P. L., "A model for dose-rate dependence of thermoluminescence intensity," J. Phys. D: Appl. Phys., 33 (2000) 846-850.
Chen, Reuven and Pagonis, Vasilis.Thermally and Optically Stimulated Luminescence - A Simulation Approach. Chichester, West Sussex: John Wiley, 2011.
Chen, R., Lawless, J.L. and Pagonis, V. "A model for explaining the concentration quenching of thermoluminescence," Radiat. Meas., 46 (2011): 1380-1384.
Chen, R., and Pagonis, V. "On the expected order of kinetics in a series of thermoluminescence (TL) and thermally stimulated peaks," Nucl. Inst. Meth. Phys. Res. B 312 (2013): 60-69.
Garlick, G. F. J. and Gibson, A. F. "The electron trap mechanism of luminescence in sulphide and silicate phosphors," Proc. Phys. Soc.60 (1948):574-590.
Groom, P. J., Durrani, S. A., Khazal, K. A. and McKeever, S.W.S. "The dose-rate dependence of thermoluminescence and sensitivity in quartz," Europ. PACT J.2 (1978): 200-210.
Halperin,A. and Braner, A. A. "Evaluation of thermal activation energies from glow curves," Phys. Rev.117 (1960): 408-415.
Horowitz, Y. S. and Yossian, D. "Computerised glow curve deconvolution: Application to thermoluminescence dosimetry,"Radiat. Prot. Dosim. 60 (1995): 1-114.
Hoogenstraaten, W. "Electron traps in ZnS phosphors,"Philips Res. Repts. 13 (1958): 515-693.
Kristianpoller, N., Chen, R. and Israeli, M. "Dose dependence of thermoluminescence peaks," J. Phys. D: Appl. Phys. 7 (1974): 1063-1074.
Lewandowski, A. C. and McKeever, S. W. S. "Generalized description of thermally stimulated processes without quasiequilibriun approximation," Phys. Rev. B,43 (1991): 8163-8178.
May, C. E. and Partridge, J. A. "TL kinetics of alpha irradiated alkali halides,"J. Chem. Phys., 40 (1964): 1401-1409.
Medlin, W. L. "Thermoluminescence properties of calcite," J. Chem. Phys. 30 (1958): 451-458.
Randall J. T. and Wilkins, M. H. F. "The phosphorescence of various solids,"Proc. Roy. Soc. London, A184 (1945):347-365.
Valladas, G. and Ferreira, J. "On the dose-rate dependence of the thermoluminescence response of quartz," Nucl. Instum. Meth. 175 (1980): 216-218.
Yukihara, E. G., Whitley, V. H., Polf, D. M., McKeever, S. W. S., Akselrod, A. E. and Akselrod, M. S. "The effect of deep trap population on the thermoluminescence of Al[math]_{2}[/math]O[math]_{3}[/math]:C,"Radiat. Meas. 37 (2003): 627-638.
Yukihara, E. G., and McKeever, S. W. S., Optically Stimulated Luminescence - Fundamentals and Applications. Singapore: John Wiley & Sons, 2011.