Förster Resonance Energy Transfer
by Dr. Martin Anderson
NIS Ltd., 588 Newport Avenue Hempstead, NY 11550, USA
Sponsored by LumiPedia
Reviewed by: Anonymous
Reviewed by: Anonymous
Date September 31st, 2019.
Contents
FRET is Fluorescence with Resonance Energy Transfer, or Fluorescence-detected Resonance Energy Transfer, or Förster Resonance Energy Transfer. It is an absorption of electromagnetic radiation by one molecule, the “donor,” followed by resonance interaction with another molecule, the “acceptor.” As a result, energy is transferred from donor to acceptor. The two molecules can be different or identical. If the two molecules are different, the process is called “hetero-transfer” (illustrated in Figure 1). If the two are identical we speak of “homo-transfer” (illustrated in Figure 2) and the energy can go back and forth for a while or go to yet another molecule until emission or a radiation-less transition takes place. FRET is extremely sensitive to the distance between the interacting molecules and can be used to visualize interactions and to measure distances between 1 and 10 nanometers.
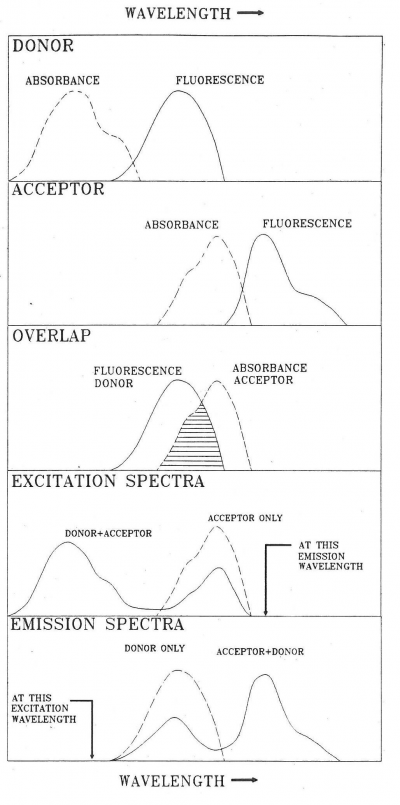
FRET can be observed in different ways. A convenient method in the case of hetero-transfer is to examine the effect of FRET on spectra of donors and acceptors as illustrated in Figure 3.
1 Acronym
The most frequently used interpretation of the acronym FRET is “Fluorescence Resonance Energy Transfer,” which is incorrect, because fluorescence is not transferred. Correct readings of FRET are “Fluorescence with Resonance Energy Transfer” (preferred by the present author [1]), or “Fluorescence-detected Resonance Energy Transfer” [2], or “Förster Resonance Energy Transfer “ [3, 4]. The phenomenon itself is Resonance Energy Transfer. RET or Resonance Energy Transfer used to be the most popular acronym [5]. Fluorescence serves to detect RET. Förster is the main force behind FRET.
2 Förster’s Contributions

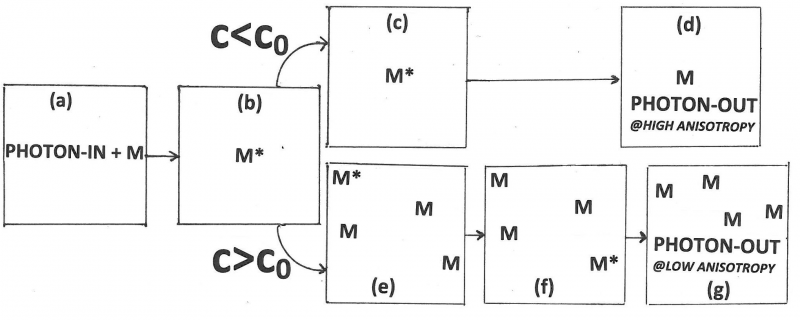
Förster’s contributions[[2]] to FRET are references 10 through 15. His 1946-paper [10] is a short preview of his 1948-paper [11]. In this preview he states the main idea in clear non-mathematical language. The 1948-paper is his most cited paper. There he focuses on FRET between like molecules (homotransfer). This type of transfer can be detected as a decrease in the polarization or anisotropy of the fluorescence with increasing concentration. Reabsorption followed by secondary emission contributes to depolarization, but it can only account for a fraction of the observed depolarization. He introduces the separation [math]R_{0}[/math] (later called the Förster distance or Förster radius; he himself called it the “critical molecular separation”), the separation distance between the donor and the acceptor at which the probability for transfer equals the combined probabilities for all other ways to deactivate the excited donor, and expresses this distance in terms of the overlap integral, the index of refraction of the medium, and the lifetime without transfer. From his data and data in the literature he calculates for fluorescein to fluorescein in water: [math]R_{0}[/math]= 5.0 nanometer, and for chlorophyll A to chlorophyll A in ethyl ether: [math]R_{0}[/math]= 8.0 nanometer. He also defines a critical concentration, [math]c_{0}[/math]c0, as the product of known constants and the inverse cube of [math]R_{0}[/math]. He made the simplification (actually, a very good approximation) that only photons emitted by the primary molecule are maximally polarized, and the ones emitted by acceptors are completely unpolarized, so that he is able to derive an equation for the polarization as a function of the concentration both for the low-concentration case and the high-concentration case. In the low-concentration limit, only the interaction between the primary molecule and one other is considered, whereas in the high-concentration limit the excitation energy is thought to diffuse away from the primary molecule. Förster also shows polarization-versus-concentration data for fluorescein in glycerin. The agreement between the data and the low-concentration curve is good up to about one-tenth of the critical concentration. Moreover, the data above the critical concentration are close to the curve derived for the high-concentration case. Finally, he briefly discusses the role of energy transfer in photosynthesis in plants where the chlorophyll concentration is about 0.1 Molar and notes that according to the theory the energy of a photon can migrate over about 10,000 chlorophyll molecules after it is absorbed by the primary molecule. His 1959 review [12] is the 10th Spiers Memorial Lecture and a translation of an earlier paper in German (Th. Förster, Z. Electrochem. 53(1949)93-104). This review is very well written and provides a conceptual understanding of FRET with a minimum of equations. He mentions the classic Bowen papers showing that FRET is different from trivial reabsorption. He compares FRET, reabsorption, donor-acceptor complex formation, and collisional quenching. He mentions three possible situations when his theory is not valid: (1) when thermal relaxation is slow, for example, in gases at low pressures, so that transfer may take place directly from the vibrational level obtained by excitation. In this case the transfer will depend on the excitation wavelength; (2) when dipole-dipole interactions are weak because of forbidden transition in the donor or acceptor; and (3) when the donor-acceptor distances are too small. This last possibility is the Dexter transfer mechanism [16].
His 1949-paper has not been translated into English. It focuses on hetero-FRET, and introduces an extension of his previous theory that predicts the time dependence of the donor fluorescence and the relation between the quantum yield of the donor and the acceptor concentration [13]. He assumes that the rate of molecular rotation is much faster than the rate of transfer, whereas the lateral diffusion is so slow that the donor-acceptor distance does not change during the transfer time. Under these conditions it is shown that the relative donor quantum yield depends only on one variable, the ratio of the acceptor concentration and the critical donor concentration. The predicted relationship between the relative donor quantum yield and this ratio was found to be in good agreement with transfer data for trypaflavine as donor and rhodamine N as acceptor in methanol. Förster uses a very clever way of excluding the effects of reabsorption in his quenching measurements: He uses a large cuvette and a small cuvette with matching concentrations such that for each data point the product of concentration times path-length is the same for both cuvettes. Consequently, the effects of reabsorption are the same in both cuvettes as long as Beer’s law holds. Therefore, the observed differences are due to FRET only.
His 1965-review [14] is not only about FRET. It is a general review of absorption, excitation, and emission. Förster distinguishes three cases. Case A refers to major alterations in absorption spectra, B to less profound changes in absorption spectra, and C to few or no alterations in these spectra. Only case C is relevant for FRET. This is the case of very weak coupling between the excited states of different molecules, where Fermi’s golden rule applies. The excitation in this case can be regarded as temporarily completely localized and excitation transfer can occur. In this review [14] he also presents a modified version of this 1948-theory [11].
His book was published in 1951 [15]. It is a superbly-written overview of fluorescence in organic substances. It describes experimental set-ups used back then. It provides data on FRET and describes the theory in great detail. One of the chapters explains how his equations can be derived from classical electromagnetic theory only, completely without quantum mechanics. This accomplishment is remarkable, because he was expected to spread the word that quantum mechanics is drastically needed in spectroscopy. Who would even consider searching for a classical derivation in his situation? There were rumors that Förster contacted radio engineers. Nobody seems to know why. One can speculate that he understood that FRET is not purely a molecular phenomenon, but that it can be scaled up to an electronic application, similar to what is now known as Near-Field-Communication. Even though FRET can be understood without quantum mechanics, an appreciation of quantum phenomena is still needed as the details of spectra and other relevant concepts in FRET can only be described using the language of quantum mechanics.
When Theodor Förster began his work on energy transfer in the late 1940‘s a significant amount of experimental information on fluorescence and quenching of fluorescence was available [1]. Even a starting point for his theory was available: Franck’s principle. This principle states that if effective energy transfer is to take place from initially excited molecules to quenching molecules, the excited states of the quenchers must be in energy resonance with the primarily excited states [17]. Oppenheimer and Arnold had pointed out that the phenomenon of resonance energy transfer, the basis of FRET, is very similar to internal conversion in radioactivity where an excited nucleus transfers energy without radiation to one of the orbital electrons resulting in ejections of this electron [4, 18, 19]. Using this similarity, they derived an expression of the rate of energy transfer for the case where the acceptors are randomly distributed around a donor. Clegg [4] showed that modifying this expression for the rate of transfer from one dominant frequency to a spectrum of frequencies leads to Förster’s famous equation for the donor-acceptor distance at which the rate of transfer equals that of donor emission, equation 3 below. However, the fact is that Oppenheimer and Arnold did not make these modifications. They did not come up with the idea of incorporating experimentally obtained spectra into their theory. Förster did [10 through 15]. This is what sets Förster apart from his predecessors and contemporaries. They all assumed one dominant frequency and ignored experimental data on spectra. Förster’s most important innovation is to incorporate experimentally obtained parameters such as spectra, quantum yield, and lifetimes into his theory, making it refutable, accessible, and extremely useful.
3 Concepts, Definitions and Equations
The “radio-analogy” is this: Emission of a photon by a molecule is very similar to broadcasting a signal from a radio sender. Absorption of a photon is like picking up a radio wave on your receiver. There are obvious differences in scale and frequencies, but the similarities are clear. FRET is analogous to NEAR-FIELD-COMMUNICATION. This technique actually uses magnetic induction and coils whereas in FRET oscillating electric dipoles interact, and here also, scale and frequencies are different, but the similarities may be helpful for building a conceptual understanding. Resonance plays an important role. Resonance is the phenomenon in which an oscillating system or an external oscillating force drives another system to oscillate with greater amplitude at special frequencies. At such frequencies (called ‘resonant frequencies”) the response is at a maximum, and small periodic driving forces can produce oscillations at large amplitudes. The simplest example is resonance in a swing, which has a natural frequency for going back and forth. Pushing the swing at this resonant frequency yields efficient transfer of energy. In FRET the resonance is electromagnetic. The excited donor contains electrons oscillating around positive centers at frequencies of the order of 10[math]^{15}[/math] Hertz. In Förster’s theory, these oscillating dipoles in the donor set up electromagnetic field and acceptors located in that field interact via resonance.
3.1 Near Field and Far Field
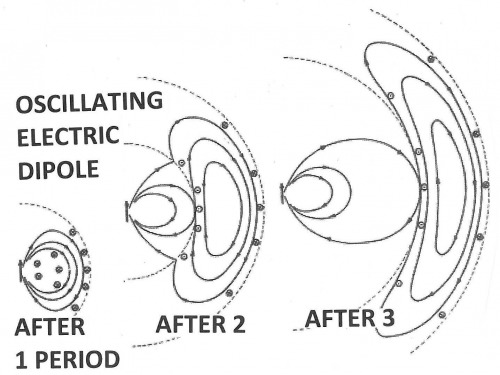
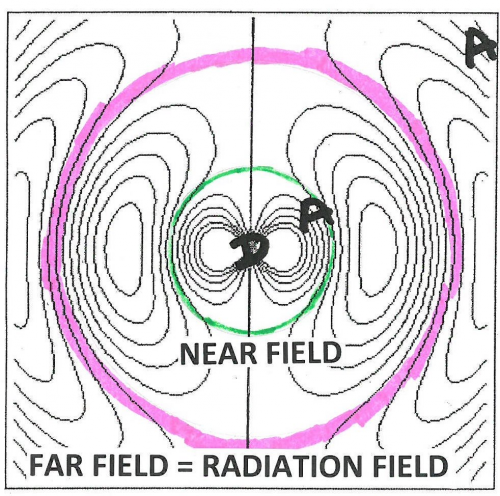
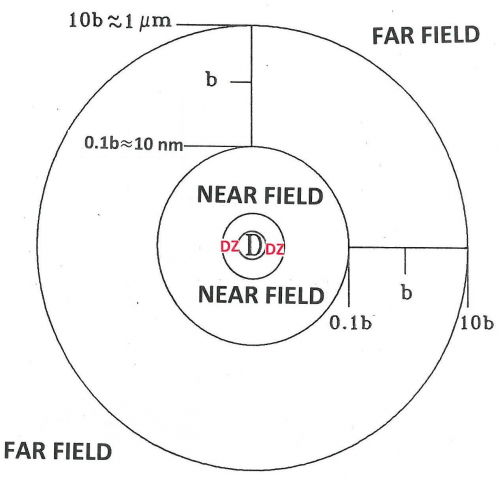
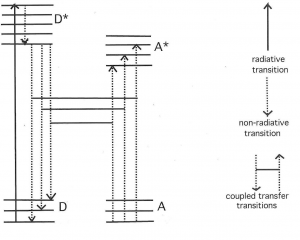
The space around these oscillating dipoles can be considered to consist of 4 parts: the contact zone (Dexter zone), the Near Field, the Intermediate Field and the Far Field (also called the Radiation Field). The contact zone is the space within about 1 nanometer from the oscillating dipole, the Near Field is the space within about 1 to 10 nanometers from it, the intermediate Field is about 10 to 1000 nanometer from it and the Far Field is beyond that. The Electric Field lines generated by an oscillating dipole form loops that are connected to the dipole in the Near Field except on the line through the dipole along the oscillation direction. These electric field lines are straight (see Figure 8). In the Intermediate Field the Electric Field lines are starting to pinch off and the pinching off is complete in the Far Field as illustrated in Figures 7 and 8.
These pinched off loops that are no longer connected to the dipole itself correspond to electromagnetic radiation, that is, photons. FRET happens in the Near Field. Absorption takes place in the Far Field (It is possible to construct a unified description of both processes, see [3] for further reading). Acceptor molecules can be anywhere. In Figure 8 two acceptors are shown (depicted as “A”), one in the Far Field and one in the Near Field. An acceptor in the Far Field is capable of absorbing radiaton emitted by the donor (“D” in Figure 8). Absorption and Emission of electromagnetic radiaton were already very well understood when Förster started his work. The absorption spectrum of the Acceptor must overlap with the emission spectrum of the Donor, otherwise the Acceptor cannot absorb this radiation (this is also resonance). The stronger the overlap the better the acceptor can pick up radiation from the donor.
An acceptor in the Near Field is capable of interacting with the electromagnetic field generated by the donor via FRET. The electric field generated by an oscillating dipole consists of three contributions, one that is proportional to 1/distance, another proportional to 1/distance-squared, and a third proportional to 1/distance-to-the-third-power [5]. The first is dominant in the Far Field and the third is the leading term in the Near Field. Here “distance” means the distance between the oscillating dipole and the point where the field exists. The electromagnetic forces in the Near Field are, therefore, very different from those in the Far Field. However, the frequency-dependence, that is, the spectral aspects of the electromagnetism generated by the excited donor in the Far Field is the same as that in the Near Field. Förster realized that he should incorporate this similarity in his theory of FRET. This idea was probably the secret of his success. The quantity that embodies this idea is R[math]_{0}[/math], the Förster distance, which is that distance at which FRET and donor fluorescence (or, actually deactivation of the donor excited state by means other than FRET) are equally probable. R[math]_{0}[/math] is defined in Equations 3 and 3A. As far as the sizes of the various zones is concerned, Figure 8 gives a rough idea. Figure 9 shows more details: the sizes of the zones depend on wavelength and the refractive index of the medium.
3.2 Quantities in Förster’s Equations
To observe FRET the following conditions must be met:
1) Donor and acceptor must have strong electronic transitions in the UV, visible, or IR,
2) Spectral overlap must exist between donor emission and acceptor absorbance,
3) Donor and acceptor must be close, but not too close,
4) The orientation factor (kappa-squared) should not be too small,
5) The donor emission should have a reasonably high quantum yield,
6) Thermal relaxation must be fast enough so that transfer takes place from the lowest vibrational level of the excited state,
7) dipole-dipole interactions must be strong enough so that forbidden interactions in donor or acceptor are irrelevant.
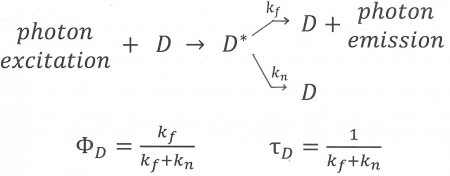
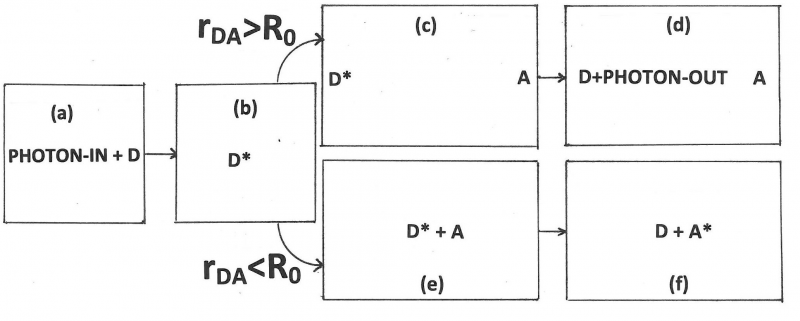
Figure 10. An illustration of the fluorescence process of the donor, D, which enters an excited state, D*, after absorption of a photon. If FRET cannot take place, there are two ways for the donor to lose its excess energy and return to the ground state: by emission (fluorescence) described by rate constant, k[math]_{f}[/math], and by a radiationless transition expressed by rate constant k[math]_{n}[/math]. Equations for the average time the donor remains excited (“lifetime of the donor in the absence of acceptor”) and the “Quantum Yield of donor fluorescence in the absence of acceptor” are also shown.
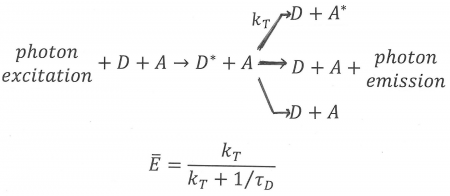
Figure 11. An illustration of FRET in the case of hetero-transfer, described by rate constant kT. Donor, D, and acceptor, A, are both present. First the donor enters an excited state, D*, after absorption of a photon. Next, FRET can take place shown here as a reaction from excited donor + acceptor to de-activated donor + excited acceptor. Note that FRET is always in competition with at least two other processes: donor emission and de-activation of the donor via a radtionless transition, both of which are shown in Figure 11. An equations for the average FRET efficiency is also shown in terms of the rate of transfer and the lifetime of the donor in the absence of acceptor, defined in Figure 11.
The following are the key quantities in Förster’s theory:
- [math]k_{T}[/math]= rate of energy transfer, indicating how often per unit of time transfer can take place; its unit is 1/second or 1/nanosecond or any convenient inverse unit of time,
- [math]\tau_{D}[/math]= lifetime of the donor excited state in the absence of acceptor, the average time the donor is excited when FRET cannot happen, often of the order of a few nanoseconds,
- [math]r_{DA}[/math]= separation distance between donor and acceptor, a center-to-center-distance, often expressed in nanometers,
- [math]R_{0}[/math]= Förster distance = Förster radius (often in nanometers) = that value of the donor-acceptor-separation at which [math]k_{T}=\frac{1}{\tau _{D}}[/math], so that at that particular distance the probability of transfer is equal to the combined probabilities of deactivation of the donor excited state by all other means,
- [math]c_{0}[/math]= critical concentration = that concentration at which transfer is equally probable to other forms of deactivation of the excited donor state,
- [math]\bar{E}[/math] = Efficiency of transfer = the most readily accessible measure of FRET can be obtained by comparing spectroscopic properties in the presence and absence of FRET. It can be determined by at least 5 different ways: by donor quenching, by acceptor sensitization, by a combination of these two, by donor photobleaching, and by acceptor photobleaching [20]. Note there is a bar above the “E”, indicating an average. In ‘Single-Molecule-FRET it is possible to measure efficiency distributions [21]. An efficiency value which is part of a distribution is indicated as [math]E[/math],
- [math]J[/math]= overlap integral, a measure of the level of resonance, defined in detail in equation 6,
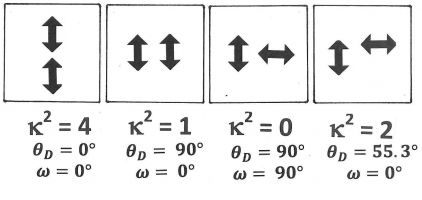
- [math]\kappa ^{2}[/math]= orientation factor, which can vary between 0 and 4, describes the interaction of the transition dipoles of donor and acceptor, as explained in Figures 12 and 13 (the possible average values of this are also relevant as explained in 3.4,
- [math]\Phi _{D}[/math]= quantum yield of the donor fluorescence in the absence of acceptor = the ratio of photons emitted by the donor to the number of photons absorbed by the donor,
- [math]n[/math]= the refractive index of the medium in which donor and acceptor are embedded.
3.3 Conditions to Observe FRET
To observe FRET, the following condition must be met:
- The donor and acceptor chromophores have strong electronic transitions in the near ultraviolet to near infrared spectral range,
- There is considerable overlap between the donor emission spectrum and the acceptor absorption spectrum as illustrated in Figure 3,
- The donor and acceptor are relatively close to each other, but not too close; the donor-acceptor separation should be roughly in the 1-10 nanometer range,
- The donor emission moment, the acceptor absorption moment, and their separation vector are in favorable mutual orientation; that is, the orientation factor, kappa-squared, should not be near zero,
- The emission of the donor has a reasonably high quantum yield.
Note that the second condition is also a requirement for transfer by reabsorption. Therefore, it is often necessary in FRET studies to correct for reabsorption effects.
3.4 Equations
Förster’s theory yield the following set of equations:
[math]\bar{E}=\frac{k_{T}}{k_{T}+\frac{1}{\tau _{D}}}=\frac{R_{0}^{6}}{R_{0}^{6}+r_{DA}^{6}}\tag{1}[/math]
[math]k_{T}=\frac{1}{\tau _{D}}\left (\frac{R_{0}}{r_{DA}} \right)^{6}\tag{2}[/math]
[math]R_{0}^{6}=\frac{9(\ln 10)\kappa ^{2}\Phi _{D}J}{128\pi ^{5}n^{4}\tau N _{A}}\tag{3}[/math]
[math]c_{0}\; for\; homo-transfer=\frac{3000}{4\pi N_{A}R_{0}^{3}}\tag{4}[/math]
[math]c_{0}\; for\; hetero-transfer=\frac{3000}{2\pi^{\frac{2}{3}}} N_{A}R_{0}^{3}\tag{5}[/math]
It is a good idea to simplify equation 3 by substituting in the values of the constants creating a “practical form” of this equation. Braslavsky et al have pointed out that there are mistakes in such practical forms all over the literature and recommend including units explicitly [22]. For example, the Förster distance can be written as in equation 3A:
[math]\frac{R_{0}}{nm}=0.02108\times \left [ \frac{\kappa ^{2}\Phi _{D}}{n^{4}}\left ( \frac{J}{M^{-1}cm^{-1}nm^{4}} \right ) \right ]^\frac{1}{6}\tag{3A}[/math]
Here the unit [math]M[/math] is [math]Molar=moles/liter=mol\times dm^{-3}[/math]. An alternative form of equation 2, often used in photosynthesis is:
[math]k_{T}=\left ( \frac{\kappa ^{2}}{r_{DA}^{6}} \right )\left ( \frac{1}{n^{4}} \right )c_{DA}\tag{2A}[/math]
with
[math]c_{DA}=\frac{9(\ln 10)\Phi _{D}J}{128\pi ^{5}\tau _{D}\tau N _{A}}\tag{2B}[/math].
This formulation of the transfer rate establishes a clear separation between geometric properties (kappa-squared/distance-to-6th-power), environmental factors (refractive index) and spectral properties ([math]c_{DA}[/math]). When [math]r_{DA}[/math] is in nanometers and [math]k_{T}[/math] is in inverse picoseconds, [math]c_{DA}[/math] is in nanometer[math]^{6}[/math]/picosecond. Another method of splitting the orientation factor off from the Förster distance is to introduce R-zero-bar:
[math]R_{0}^{6}=\frac{2}{3}\kappa ^{2}\bar{R_{0}^{6}}\tag{3B}[/math]
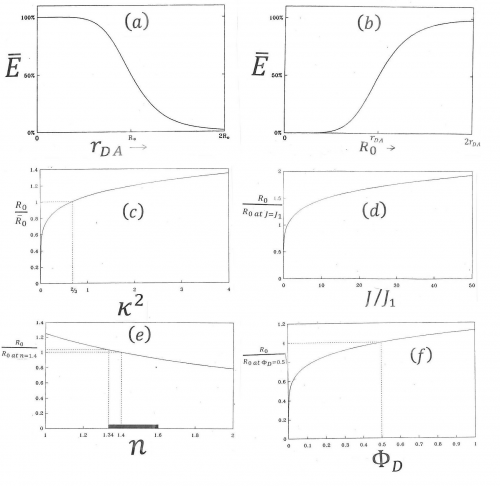
where [math]R_{0}[/math]-with-bar-on-top is defined as the Förster distance when kappa-squared equals its average value, 2/3. Kappa-squared is explained in Figures 12 and 13. Figure 14 illustates characteristics of equation 1 and 3.
3.5 Orientation Factor and Overlap Integral
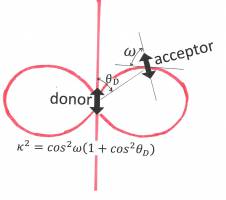
Figure 12. The orientation factor, kappa-squared, depends on the relative orientations of the donor “atomic-antenna” (transition moment, depicted as a double-headed arrow in the center), that of the acceptor “atomic-antenna” (the other double-headed arrow), and that of the line connecting their centers (line connecting the centers of the arrows). The angle [math]\theta _{D}[/math] is between the donor “antenna” and the connection line. The angle [math]\omega[/math] is between the connection line and the electric field generated by the donor at the position of the acceptor. This factor is given given as [math]\kappa ^{2}=\cos ^{2}\omega (1+\cos ^{2}\theta _{D})[/math]. Its value is between 0 and 4. Kappa-squared equals 0 whenever the acceptor “atomic-antenna” is perpendicular to the electric field line (in the plane of the paper or perpendicular to that plane), and it is 4 if both donor and acceptor are parallel to the connection line.
Figure 13. A few specific examples of configurations with different kappa-squared-values. Both donor and acceptor transition moments are indicated as double-headed arrows. It is not necessary to show which of the two is the donor or the acceptor, as kappa-squared is invariant when the donor transition moment and the acceptor transition moment are interchanged.
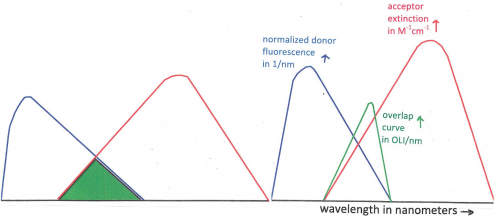
The overlap integral is illustrated in Figure 15, and depends on wavelength,[math]\lambda[/math], the donor fluorescence spectrum normalized on the wavelength scale, [math]f_{D}(\lambda)[/math] , and [math]\epsilon _{A}(\lambda )[/math] the molar extinction coefficient of the acceptor,
[math]J=\int f_{D}(\lambda )\epsilon _{A}(\lambda )\lambda ^{4}d\lambda\tag{6}[/math]
This integral extends over the region that encompasses the line shapes of the relevant donor emission and acceptor absorption bands. A convenient unit for the overlap integral is OLI = 10[math]^{14}[/math]M[math]^{-1}[/math]cm[math]^{-1}[/math]nm[math]^{4}[/math] = 10[math]^{-14}[/math]M[math]^{-1}[/math]cm[math]^{3}[/math] [1,23]. Wavelength is most often expressed in nanometers, is usually in M[math]^{-1}[/math]cm[math]^{-1}[/math], and has the unit nm-1 and is defined by equation 7:
[math]f_{D}(\lambda )=\frac{F_{D\lambda }(\lambda )}{\int F_{D\lambda }d\lambda } \tag{7}[/math]
where [math]F_{D\lambda }[/math] is the donor fluorescence per unit of wavelength interval and the integral extends over the relevant donor emission band(s). The overlap integral can alternatively be expressed in wavenumber form or in frequency form [1].
4 Innovations, Trends and Applications
Many topics in FRET deserve special attention. New technologies and new subfields have opened up allowing for novel applications.
4.1 Dexter Transfer
There are other transfer mechanisms besides FRET. Masters gives a nice overview of similarities and differences between the Förster mechanism and the Dexter process [8]. As shown in Figure 9 there is the Near Field and the Dexter Zone. The Near Field is about 1 to 10 nanometers from the donor, but the Dexter Zone is where donor and acceptor practically touch each other. Many inorganic systems exhibit energy transfer mediated by triplet-triplet interactions and energy transfer mitigated by such interactions can be described by Dexter’s theory [16]. This theory is based on exchange interactions [16, 24] and predicts a rate of transfer with a distance dependence as in equation 8
[math]k_{Dexter}=constant\times e^{-2r_{DA}/L}\tag{8}[/math]
where L is the sum of the van der Waals radii of the donor and the acceptor and [math]r_{DA}[/math] is the center-center-separation-distance between donor and acceptor. A new generalized Förster-Dexter theory of intramolecular energy transfer for systems which have discrete or quasicontinuous initial and final states has been developed [25]. The authors of this theory express the rate constant for energy transfer in terms of molecular parameters such as electronic energy gap and free energy change. Combined Förster-Dexter transfer has potential for the development of chemosensors [26].
4.2 Depolarization Factors
Often, the transition moment of the donor fluctuates around an orientation called the “donor axis”. Similarly, the transition moment of the acceptor fluctuates around an “acceptor axis”. If the rates of these fluctuations are high compared to the rate of transfer, the kappa-squared in the equations for R[math]_{0}[/math] (equations 3, 3A and 3B) can be replaced by an average-kappa-squared. Dale, Eisinger and Blumberg pointed out that this average kappa-squared depends on “depolarization factors” that can be measured using fluorescence anisotropy (or fluorescence polarization data) [27]. And, that one can experimentally verify whether or not replacing kappa-sqared by 2/3 is correct. If both the donor fluorescence and the acceptor fluorescence are completely depolarized, it is safe to perform this replacement, but if these are highly polarized such a simplifications can give rise to significant errors. The average kappa-squared is given in equation 9, in terms of the depolarization factors for the donor [math]d[/math], [math]a[/math]for the acceptor, and angles [math]\Theta_{D}[/math], [math]\Theta_{A}[/math] and [math]\Phi [/math]. Details about the minimum and maximum kappa-squared and the most probable value of this orientation factor in the dynamic averaging regime can be found at [www.fretresearch.org]. Visualization of the average kappa-squared and its dependence on the various angles and depolarization factors can be found at [4].
[math]\left \langle \kappa ^{2}\right \rangle=\frac{2}{3}-\frac{1}{3}(d+a)+d(1-a)\cos ^{2}\Theta _{D}+a(1-d)\cos ^{2}\Theta _{A}+ad\kappa _{1,1}^{2}\tag{9A}[/math]
[math]\kappa _{1,1}^{2}=(\sin \Theta _{D}\sin \Theta _{A}\cos \Phi-2\cos \Theta _{D}\cos \Theta _{A} )^{2}\tag{9B}[/math]
Errors in the donor-acceptor-separation estimated from FRET with uncertainties in the orientation factor, distributions of kappa-squared and apparent separation distances are discussed in references 28, 29, 30 and at [www.fretresearch.org].
4.3 Averaging Regimes
When using equation 1 it is often necessary to take averages. There are at least two different methods of taking averages depending on which “averaging regime” applies. The two relevant regimes are the “dynamic averaging regime” and the “static averaging regime”. The dynamic averaging regime refers to the situation where both donor and acceptor can take up their entire range of orientations within the lifetime of the excited state of the donor and the donor-acceptor-separation can have low-amplitude fluctuations around its average value so that [math]r_{DA}[/math] is essentially unique. In this regime the average transfer efficiency is given by equation 10, a modified version of equation 1:
[math]\bar{E}=\left \langle E \right \rangle_{dynamic}=\frac{\frac{2}{3}\left \langle \kappa ^{2} \right \rangle \bar{R_{0}^{6}}}{\frac{2}{3}\left\langle \kappa ^{2} \right \rangle \bar{R_{0}^{6}}+r_{DA}^{6}}\tag{10}[/math]
In this case the average of kappa-squard is given by equation 9. If both depolarization factors are zero, the average kappa-squared is equal to 2/3, which case is known as the “isotropic dynamic regime”.
On the other hand, when the rate of rotations and/or the rate of translations is (are) much smaller than the rate of transfer, the “static averaging regime” applies and the efficiency must be averaged over distributions applicable to the situation at hand:
[math]\bar{E}=\left \langle E \right \rangle_{static}=\left \langle \frac{\frac{2}{3}\kappa ^{2} \bar{R}_{0}^{6}}{\frac{2}{3}\kappa ^{2} \bar{R}_{0}^{6}+r_{DA}^{6}} \right \rangle\tag{11}[/math]
A completely different situation is the Rapid Diffusion Limit.
4.4 Rapid Diffusion Limit
If the donor-acceptor separation can change during the lifetime of the donor’s excited state as a result of lateral diffusion, FRET can be enhanced. If the relative distance covered during this lifetime is much larger than the mean donor-acceptor separation, th system is said to be in the rapid diffusion limit, where the efficiency approaches a maximum value that depends primarily on the distance of shortest approach and is insensitive to minor changes in the diffusion constans of the donor or accpor. To reach this limit, donor lifetimes of the order of millisecond are needed [31]. Thomas, Carlsen and Stryer have applied diffusion-enhanced FRET to elucidate the position of the retinal chromophore of rhodopsin in retinal disc membranes [32]. They find that the distance of closest approach between terbium dipicolinate and retinal is 2.2 nm from the intradisc surface and 2.8 nm from the external surface of the disc membranes. They estimate the precision of the method to be of the order of 0.1 to 0.2 nm. However, factors such as irregularities of the membrane surfaces and electrostatic interactions can worsen the precision somewhat [32]. Rapid-diffusion FRET, also known as diffusion-enhanced FRET, is reviewed by Stryer, Thomas and Meares [33].
4.5 Efficiency in the Static Averaging Regime
Equation 11 and equation 1 are not consistent with each other. Equation 1 refers to the simplest case where there is one unique distance between the donor and acceptor, and one average value for the orientation factor. An interesting case is the model where the donor-acceptor-separation is unique but the orientation factor can have all values between 0 and 4 at the same time, so that the absolute value of cosine of omega in Figure 12 is random between 0 and 1, and the same is true for the cosine of theta-D in that Figure. We will call this theoretical model the “all-orientations-one-separation-model”. For this and other cases described by equation 11, the following generalization of equation 1 can be used:
[math]\left \langle k_{T}\tau _{D} \right \rangle=\frac{2}{3}\left \langle \kappa ^{2} \right \rangle \left ( \frac{\bar{R}_{0}}{\bar{r_{DA}}} \right )^{6}=\frac{\bar{E}}{(1-\bar{E})^{N}}\tag{12}[/math]
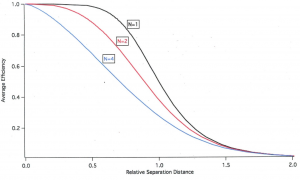
Here the first equals-sign defines the separation-from-average-transfer-rate, [math]r_{DA}[/math]. The brackets [math]\left \langle \cdot \right \rangle[/math] represent averages over an appropriate distribution, and N can depend on the average efficiency, [math]\bar{E}[/math]. For the all-orientations-one-separation-model equation 12 can be simplified as the average of kappa-squared in that case is equal to 2/3. This model was first studied by Dale. He showed that N=2 is a very good approximation for the all-orientations-one-separation-case [34]. Vogel et al. have proposed that equation 12 with N=2 and <kappa-squared> = 2/3 can be used to estimate the distance between Fluorescent-Protein-FRET-pairs [35]. By taking the natural logarithm in equation 12, it is possible to plot the average-efficiency versus [math]\bar{r}_{DA}/\bar{R_{0}}[/math] the “relative separation distance”. Figure 16 shows this relationship for N = 1 (the Förster equation), N = 2 (for the all-orientations-one-separation model), and N = 4 (an unusual case described in Table 1 as the “N=4-distribution”). The point of Figure 16 is that, if a static distribution of transfer rates exists, the Förster equation overestimates the donor-acceptor separation distance. The wider the distribution, the bigger the N and the more pronounced the deviation from the Förster equation for efficiency values in the 0.2-0.9 range. In general N will depend on the efficiency. As shown in Table 1, for the “spherical-ring-model” the N value near E=0 is much larger than that near E=1. In this case the donor-acceptor separation vector is random between two spheres representing the minimum and maximum distance. A similar trend is also shown for the rectangular and triangular distributions. On the other hand, N is essentially independent of the efficiency for the all-orientations-one-separation model) and for the N=4-distribution. It can be shown that the value for N near very low efficiency values is equal to the average of the square of the transfer rate divided by the square of the average rate. This value can be obtained from time-resolved-efficiency measurements, that is, TRE-curves. Such graphs for the Time-Resolved-Efficiency are available for the all-orientations-one-separation-model. These are similar to experimental TRE curves for some Fluorescent-Protein-Donor-Acceptor-pairs [30]. (for further reading see www.fretresearch.org[5])
| TABLE 1: N in equation 12 and Figure 16 depends
on the type of distribution and, in general, depends also on the value of the average efficiency | |||||
|---|---|---|---|---|---|
| Model of distribution | Equation in terms of [math]x=k/\bar{k}[/math] where [math]k[/math]=transfer rate and [math]\bar{k}[/math]=average transfer rate. | N @E=0 | N@E=0.5 | N@E=0.9 | N@E=1 |
| Rectangular peak | [math]p(x)=1/(2A)[/math] for [math]A-1\leq x\leq 1+A[/math], [math]p(x)=0[/math] for other values of [math]x[/math]. [math]A[/math] describes width of distribution and varies between 0 (delta-peak) and 1 (wide peak) with [math]0\leq x\leq 2[/math]. | 1.08 for [math]A[/math]=0.5 and 1.33 for [math]A[/math]=1 | 1.06 for [math]A[/math]=0.5 and 1.32 for [math]A[/math]=1 | 1.04 for [math]A[/math]=0.5 and 1.3 for [math]A[/math]=1 | 1.0 for [math]A[/math]=0.5 and 1.0 for [math]A[/math]=1 |
| Triangular peak | [math]p(x)=(x-1+A)/A^{2}[/math] for [math]A-1\leq x\leq 1[/math] and [math](A+1-x)/A^{2}[/math] for [math]1\leq x\leq 1+A[/math] and zero for other [math]x[/math] values. [math]A[/math]describes width of distribution and varies between 0 (delta-peak) and 1 (wide peak) with [math]0\leq x\leq 2[/math]. | 1.04 for [math]A[/math]=0.5 and 1.17 for [math]A[/math]=1 | 1.03 for [math]A[/math]=0.5 and 1.14 for [math]A[/math]=1 | 1.02 for [math]A[/math]=0.5 and 1.10 for [math]A[/math]=1 | 1.0 for [math]A[/math]=0.5 and 1.0 for [math]A[/math]=1 |
| Separation distance is unique, but kappa-squared
assumes all values between 0 and 4 |
[math]p(x)=\frac{\ln (2+\sqrt{3})}{3\sqrt{2x}}[/math] for [math]0\leq x\leq \frac{3}{2}[/math]
[math]p(x)=\frac{\ln \left ( \frac{2+\sqrt{3}}{\sqrt{\frac{2x}{3}}+\sqrt{\frac{2x}{3}}-1} \right )}{3\sqrt{2x}}[/math] for [math]\frac{3}{2}\leq x\leq 6[/math] |
2.16 | 2.8 | 1.98 minimum value, but for all E
N[math]\approx[/math]2 |
2.0 |
| N=4-distribution | [math]p(x)=0.1962x^{-3/4}[/math] for [math]0\leq x\leq 1[/math]
[math]p(x)=0.03689[/math] for [math]1\leq x\leq 6.834[/math] and [math]p(x)=0[/math] for other [math]x[/math] values This is not a realistic distribution, but an artificial case designed to yield [math]N\approx 4[/math] for all efficiency values |
4.0 | 3.9 | 3.8 minimum value @ E=0.84 | 4.0 |
| Spherical Ring model | [math]p(x)=\frac{\sqrt{M^{3}}}{2(M^{3}-1)x\sqrt{x}}[/math] for [math]M^{-3}\leq x\leq M^{3}[/math]
[math]M[/math] describes the width of the distribution: The donor-acceptor separation vector is random between 2 spheres. The radius of the outer sphere (maximum distance) is [math]M[/math] times the radius of the inner sphere (minimum distance). [math]distance\; from\; average\; rate=minimum\times \sqrt{M}=maximum/\sqrt{M}[/math] |
9.2 for [math]M[/math]=3 and 3.2 for [math]M[/math]=2 | 3.5 for [math]M[/math]=3 and 2.0 for [math]M[/math]=2 | 2.3 for [math]M[/math]=3 and 1.4 for [math]M[/math]=2 | 1.0 for [math]M[/math]=3 and 1.0 for [math]M[/math]=2 |
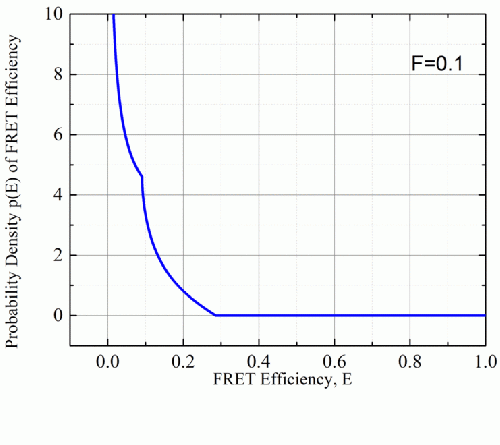
FRET efficiency distributions can be measured using single-molecule FRET [21]. Comparing these with theoretical cases is of interest. For example, the efficiency distribution for the “all-orientations-one-separation-model” shows one single peak at relatively large separation distances but two peaks at lower distances. The parameter [math]F[/math], defined as [math]F=\frac{3}{2}\left ( \frac{\bar{R_{0}}}{\bar{r_{DA}}} \right )^{6}[/math] determines the strength fo the interaction. The minimum efficiency value is always zero, but the maximum value depends on F and is equal to 4F/(1+4F), corresponding to kappa-squared is 4. For F > 1/3, the distribution has two peaks: a low efficiency and a high efficiency peak. The existence of two peaks in such distributions can be easily misunderstood as corresponding to two different donor-acceptor-separation distances. However, in this case such an interpretation is clearly false as the assumption of the model is that there is one unique separation distance. The variation in orientations via kappa-squared determines the characteristics of the distribution. The description of this distribution can be expressed using two factors G and H, defined in equations 13a and 13b. The probability frequency distribution is given in 13c in terms of the efficiency and G and H.
[math]G=\sqrt{\frac{E}{F(1-E)}}\tag{13A}[/math]
[math]H=\frac{1}{2(1-E)\sqrt{3EF(1-E)}}\tag{13B}[/math]
[math]p(E)=\left\{\begin{matrix}
H\ln (2+\sqrt{3})\;\: \: \: \: \: \: \: \: \: \: \: 0\leq E\leq \frac{F}{1+F} & \\
H\times \ln \frac{2+\sqrt{3}}{G+\sqrt{G^{2}-1}}\;\: \: \: \: \: \: \: \: \: \: \: \: \: \frac{F}{1+F}\leq E\leq \frac{F}{1+4F} & \\
0\;\: \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \frac{F}{1+4F}\leq E &
\end{matrix}\right.\tag{13C}[/math]
4.6 Science and Technology Linked to FRET
Theodor Förster has inspired, partly, directly or indirectly, several new areas of science and technology as listed in Table 2.
| TABLE 2:New Areas of Science inspired by
Theodor Förster’s work on FRET |
|---|
| Energy Transfer in Photosynthesis |
| Structure of Bio-Macro-Molecules |
| Imaging With Fluorescent Proteins |
| Imaging With Quantum Dots |
| Nanotechnology |
| Single Molecule Studies |
Arguably the most important of these new fields in science and technology are Imaging with Fluorescent Proteins and Quantum Dots.
- Energy Transfer in Photosynthesis
Knox has adopted the working hypothesis that Förster’s mechanism for energy transfer is applicable to all phenomena of interest to photosynthesis [37]. Van Grondelle, Dekker, Gillbro and Sundstrom have reviewed the mechanisms of excitation energy transfer and trapping in photosynthetic systems [38].
- Structure Of Bio-Macro-Molecules
The Stryer-Haugland-paper of 1967 can be considered to the starting point of FRET applications in molecular biochemistry and biophysics[39]. They presented a systematic study of the dependence of energy transfer efficiency on the donor-acceptor-separation distance, using L-proline oligopeptides as spacers of defined length. A naphthylamide donor and a 1,5-dansyl acceptor were attached to the ends of an oligopeptide consisting of N proline units with N varying between 1 and 12. Optical rotatory dispersion measurements indicate that the oligomers from N=5 to N=12 are tj etu[e II trans helix conformation. Consequently, the donor-acceptor separation could be accurately calculated from coordinates available in the literature for this system, with an estimated uncertainty of about 0.3 nanometer. The efficiency of energy transfer decreased from 100% for N=1 at a distance of 1.2 nm to a value of 16% for N=12 at 4.6 nm, and 50% efficiency occurred at 3.46 nm. The plot of LN(inverse efficiency minus 1) versus LN(distance) is linear with a slope of 5.9[math]\pm[/math]0.3, in excellent agreement with Förster’s prediction. Stryer published a beautiful review of proximity relations from FRET in rhodopsin, galactose receptor protein, metalloproteins, cytochrome c oxidase, pyruvated dehydrogenase complex, ribosomes, transfer RNA, membrane channels and pumps, and flexible polypeptides [40]. A detailed overview of FRET tecniques and results on folding and conformational changes in biological structures is available [41].
- Imaging with Fluorescent Proteins
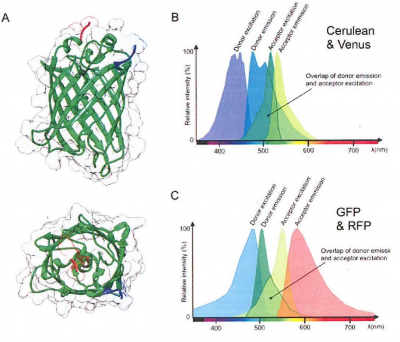
The Nobel Prize in Chemistry for 2008 was awarded jointly to Osamu Shimomura [42], Martin Chalfie [43] and Roger Tsien [44] for the discovery and development of the green fluorescent protein, GFP. Not only the Green FP, but also Yellow, Red and many more Fluorescent Proteins are available [45]. They have provided science with an abundance of tools, many of which are based on FRET, for the imaging of subcellular structures, protein dynamics, metabolite concentrations, and enzyme activities in live cells [45]. Information on structure and spectra is shown in Figure 18.
- Imaging with Quantum Dots
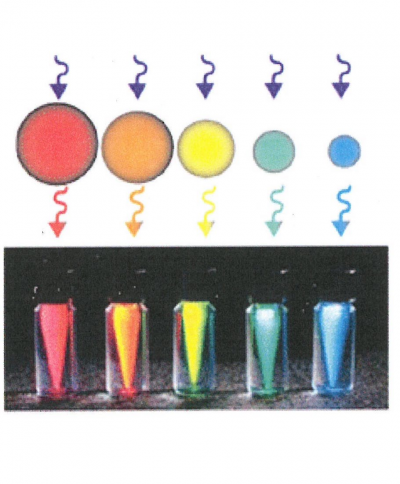
As reviewed by Algar, Massey and Krull [47], Brus and coworkers at Bell Labs reported the first colloidal Quantum Dots [48]. For cellular imaging the key papers are references 49 and 50, both published in 1998 [47]. Water-soluble, photoluminescent CdSe/ZnS core/shell Quantum Dots were prepared and used for cellular imaging [49, 50]. Quantum Dots have unique optical properties: strong and broad absorption spectra, narrow photoluminescence that can be tuned by choices of size and composition, high quantum yields, good photostability [47]. Figure 19, adapted from reference 51, illustrates some of these characteristics. FRET-based applications include: immunoassays, hybridization assays, enzyme assays, sensors for metabolites and drugs, pH sensing, tracking therapeutic delivery, photodynamic therapy, cellular imaging and light harvesting [47].
- Nanotechnology
The use of FRET in Nanotechnology has been reviewed by Albinsson and Hannestad [52]. Of particular interest is Multistep FRET or Energy Migration, where there is not just one donor and one acceptor, but multiple fluorophores are involved so that the excitation of an initial donor triggers a chain of FRET events passing through multiple chromophores. All the chromophores can be of one species (multistep homotransfer) or they can be differen (multistep heterotransfer) [52]. Of particular interest is the concept of a “photonic wire”, which is a linear arrangement of fluorophores so that energy can be transferred from one end to the other via FRET. The first example of such a photonic wire consisted of an input dye, BODIPY, three zinc porphyrins and a free-base porphyrin covalently connected through diarylethyne linkers [53]. Channeling energy to predetermined sits on a DNA-based nano system is now possible [52]. Advances in microfluidics, nanotechnology, and materials have the potential to revolutionize FRET-based assays with applications in personalized medicine [54]. Applications of FRET in immunology are note-worthy [55].
- Single Molecule Studies
Major pregress in fluorescence microscopy instrumentation and detection sensitivity has made it possible to observe FRET at the single molecule level. One of the first single-molecule-FRET (smFRET) studies was about the folding of chymotrypsid inhibitor 2, a single-domain protein [56]. A wide variety of smFRET methods may be used. Solution measurements are fastest and easiest to perform, but several techniques are now available to immobilize the labeled molecules on a substrate with minimal perturbation of their function and characteristics [57].
5 References
[1] VanDerMeer, B. Wieb “Förster Theory” In FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 23-62. Weinheim Germany: Wiley-VCH, 2014.
[2] Vanbeek, D.B., M.C. Zwier, J.M. Shorb, and B.P. Krueger. “Fretting about FRET: Correlation between κ and R.” Biophysical Journal 92(2007):4168-4178.
[3] Medintz, Igor, and Niko Hildebrandt, editors, FRET - Förster Resonance Energy Transfer From Theory to Applications Weinheim Germany: Wiley-VCH, 2014.
[4] Clegg, Robert M. “The History of FRET.“ In Reviews in Fluorescence, volume 3, edited by C.D. Geddes and J.R. Lakowicz, 1-45. Springer International Publishing Switzerland 2014.
[5] VanDerMeer, B. Wieb, George Coker, III, and S.-Y. Simon Chen, Resonance Energy Transfer. Theory and Data, New York, Weinheim and Cambridge, VCH Publishers, 1994.
[6] Weller, H. “Nachruf auf Theodor Förster.” Berichte der Bunsengesellschaft für Physicalische Chemie 78(1974):969-971.
[7] Weller, H. “In Memoriam, Theodor Förster, 1910-1974.” EPA Newsletter 9(1980):6-19.
[8] Masters, B.R. “Paths to Förster’s resonance energy transfer (FRET) theory.” Eur. Phys. J. H. 39(2014): 87-139, DOI: 10.1140/epjh/e2013-40007-9
[9] Dreeskamp, Herbert, “How I Remember Theodor Förster” In FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 3-8. Weinheim Germany: Wiley-VCH, 2014.
[10] Förster, Th. “Energiewanderung und Fluoreszenz” Naturwissenschaften, 33(1946):166-175; translated by Klaus Suhling “Energy Migration and Fluorescence.” Journal of Biomedical Optics, 17(2012):01101-1-01102-10.
[11] Förster, Th. “Zwischenmolekulare Energiewanderung und Fluoreszenz” Annalen der Physik, 2(1948)55-75; translated by E.V. Mielczarek, E. Greenbaum, and R.S. Knox, editors, “Intermolecular Energy Migration and Fluorescence.” Biological Physics, 148-160, New York, American Institute of Physics, 1993.
[12] Förster, Th. “Transfer Mechanisms of Electronic Excitation” Discussions of the Faraday Society, 27(1959):7-17, adapted from Förster,Th, Z. Electrochem. 53(1949):93-104.
[13] Förster, Th. “Experimentelle und theoretische Untersuching des zwischenmoleulcaren Übergangs von Elekronenanregungsenergie” Zeitschrift für Naturforschung, 4a(1949):321-327.
[14] Förster, Th. “Delocalized Excitation and Excitation Transfer,” In Modern Quantum Chemistry edited by Sinanoğlu, 93-137. New York, Academic Press, 1965.
[15] Förster, Th. Fluoreszenz Organischer Verbindungen, Göttingen, Vandenhoek and Ruprecht, 1951.
[16] Dexter, D.L. “A theory of sensitized luminescence in solids.” J. Chem. Phys. 21(1953):836-850.
[17] Franck, J. “Einige aus der Theorie von Klein und Bosseland zu ziehende Folgerungen über Fluoreszenz, photochmische Prozesse und die Electronenemission glühender Körper.” Zeitschrift für Physik 9(1922):259-266.
[18] Oppenheimer, J. R. “Internal Conversion in Photosynthesis.” Phys. Rev. 60(1941):158.
[19] Arnold, W., and J. R. Oppenheimer. “Internal Conversion in photosynthetic mechanism of blue-green algae.” J. Gen. Physiol. 33(1950):423-435.
[20] Hildebrandt, Niko “How to apply FRET: From Experimental Design to Data Analysis.” In FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 105-163. Weinheim Germany: Wiley-VCH, 2014.
[21] Pons, Thomas “Single-Molecule Applications.” In FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 105-163. Weinheim Germany: Wiley-VCH, 2014.
[22] Braslavsky, S.E., E. Fron, H.B. Rodriguez, E. San Roman, G.D. Scholes, G. Schweitzer, B. Valeur, J. Wirz. “Pitfalls and Limitations in the Practical Use of Förster’s Theory of Resonance Energy Transfer.” Photochem. Phtotbiol. Sci. 7(2008):1444-1448.
[23] Byrne, A.G, M.M. Bynre, G. Coker III, K.B. Gemmel, C. Spillmann, I. Medintz, S.L. Sloan, and B.W. VanDerMeer “Data.” In FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 657-755. Weinheim Germany: Wiley-VCH, 2014.
[24] Scholes. G.D. “Long-range Resonance Energy Transfer in Molecular Systems.” Annu. Rev. Phys. Chem. 54(2003):57-87.
[25] Lin, S.H., W. Z. Xiao, W. Dietz. “Generalized Förster-Dexter Theory of Photoinduced Intramolecular Energy Transfer.” Phys. Rev. E 47(1993)36798-3706.
[26] Murphy, C.B., Y. Zheng, T. Troxler, V. Ferry, J.J. Martin, and W.E. Jones. “Probing Förster and Dexter energy-transfer Mechanisms in Fluorescent Conjugated Polymer Chemosensors.” J. Phys.Chem. B 106(2004)1537-1543.
[27] Dale, R.E., J. Eisinger, and W.E. Blumberg. “The Orientation Factor in Intramolecular Energy Transfer.” Biophys. J. 26(1979)161-194.
[28] VanDerMeer, B.W. “Orientational Aspects in Pair Energy Transfer.” In Resonance Energy Transfer edited by D. L. Andrews and A.A. Demidov, 151-172. New York, John Wiley & Sons, 1999.
[29] VanDerMeer, B.W. “Kappa-squared: from nuisance to new sense.” Reviews in Molecular Biotechnology 82(2002):181-196., 151-172.
[30] VanDerMeer, B. W., D.M. van der Meer, and S.S. Vogel. “Optimizing the Orientation Factor Kappa-Squared for More Accurate FRET Measurements.” In FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 63-104. Weinheim Germany: Wiley-VCH, 2014.
[31] Thomas, D.D., and L. Stryer. “Transverse Location of the RetinalChromophore of Rhodopsin in Rod Outer Segment Disc Membranes.” J. Mol. Biol. 154(1982):145-157.
[32] Thomas, D.D., W.F. Carlsen, W, and L. Stryer. “Fluorescence Energy Transfer in the Rapid-Diffusion Limit.” Proc. Natl. Acad. Sci. U.S.A. 75(1978):5746-5750.
[33] Stryer, L., D.D. Thomas, and C.F. Meares. “Diffusion-Enhanced Fluorescence Energy-Transfer.” Ann. Rev. Biphys. Bioeng. 11(1982):203-222.
[34] Dale, R.E. “Fluorescence depolarization and orientation factors for excitation-energy transfer between isolated donor and acceptor fluorophore pairs at fixed inter-molecular separations.” Acta Physica Polonica A 54(1978):743-756.
[35] Vogel, S.S., B.W. VanDerMeer, and P.S. Blank. “Estimating the distance separation florescent protein FRET pairs.” Methods 65(2014):131-138, https://doi.org/10.1016/j.ymeth.2013.06.021
[36] Vogel, S.S., T.A. Nguyen, B.W. VanDerMeer, and P.S. Blank. “The Impat of Heterogeneity and Dark Acceptor States on FRET: Implications for Using Fluorescent Protein Donors and Acceptors.” PLoS ONE 7(11) e49593. https://doi.org/10.1371/journal.pone.0049593
[37] Knox,R.S. “Excitation Energy Transfer and Migration: Theoretical Considerations.” In Energetics of Photosynthesis edited by Govindjee, 183-220. New York San Fransisco London: Academic Press, 1975.
[38] Van Grondella, R., J.P. Dekker, T. Gillbro, and V. Sundstrom. “Energy Transfer and Trapping in Photosynthesis.” Biochim. Biophys. Acta – Bioenergentics 1187(1994):1-65. [39] Stryer, L., and R.P. Haugland. “Energy Transfer: A Spectroscopic Ruler.” Proc. Natl. Acad. Sci. USA 58(1967):716-726.
[40] Stryer, L. “Fluorescence Energy Transfer as a Spectorscopic Ruler.” Ann. Rev. Biochem. 47(1978): 819-846.
[41] Robinson, Philip J., and Chryl A. Woolhead. “Implemeentation of FRET Technologies for Studying the Folding and Confromational Changes in Biological Structures.” In FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 357-396. Weinheim Germany: Wiley-VCH, 2014.
[42] Shimomura, O., F.H. Johnson, and Y. Saiga. “Extraction, purification and properties of aequorin, a bioluminescent protein from luminour hydromedusan, Aequaorea.” Jounal of Cellular and comparative Physiology 59(1962):223-239.
[43] Chalfie, M., Y. Tu, G. Euskirchen, W.W. Ward, and D.C. Prasher. “Green Fluorescent Protein as a marker for gene expression.” Science 263(1994):802-805.
[44] Heim, R., D.C. Prasher, and R.Y. Tsien. “Wavelength mutations and posttranslational autoxidation of Green Fluorescent Protein.” Proc. Natl. Acad. Sci. USA 91(1994): 12501-12504.
[45] Hai, Hiofan, Yidan Ding, and Robert E. Campbell. “FRET with Fluorescent Proteins.” In FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 433-473. Weinheim Germany: Wiley-VCH, 2014.
[46] Hochreiter, B., A.P. Garcia, and J.A. Schmid. “Fluorescent Proteins as Genetically Encoded FRET Biosensors in Life Sciences.” Sensors 15(10)(2015): 26281-26314; doi:10.3390/s151026281 http://www.mdpi.com/1424-8220/15/10/26281/htm
[47] Algar, W. Russ, Melissa Massey, and Ulrich J. Krull. “Semiconductor Quantum Dots and FRET.” In FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 475-585. Weinheim Germany: Wiley-VCH, 2014.
[48] Rossetti, R., S. Nakahara, and L.E. Brus. “Quantum size effects in the redox potentials, resonance Raman spectra, and electronic spectra of CdS crystallites in aqueous soutions.” J.Chem.Phys. 79(1983):1086-1088.
[49] Chan, W.C.W., and S. Nie. “Quantum dot bioconjugates for ultrasensitive nonisotropic dectection.” Science 281(1998):2016-2018.
[50] Bruchez, M., M. Moronne, P. Gin, S. Weiss, and A.P. Alivisatos. “Semiconductor nanocrystals as fluorescent biological labels.” Science 281(1998):2013-2016.
[51] Semrock, Inc, 3625 Buffalo Road, Suite 6, Rochester, New York 14624 [6].
[52] Albinsson, Bo, and Jonas K. Hannestad. “MultistepFRET and Nanotechnology.” In FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 607-653. Weinheim Germany: Wiley-VCH, 2014.
[53] Wagner, R. W. and J.S. Lindsey. “A molecular photonic wire.” Journal of the merican Chemical Society 116(1994):9759-9760.
[54] Spindel, Samantha, Jessica Granek, and Kim E. Sapsford. “In Vitro FRET Sensing, Diagnostics, ad Personalized Medicine.” In FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 271-305. Weinheim Germany: Wiley-VCH, 2014.
[55] Szöllosdi, J., V. Horejsi, L. Bene, P. Angelisova, and S. Damjanovich. “Supramolecular complexes of MHC class I, MHC class II, CD20, and tetraspan molecules (CD53, CD81, and CD82) at the surface of a B cll line JY.” Journal of Immunology 157(1996)2939-2946.
[56] Deniz, A.A., T.A. Laurence, G.S. Beligere, M. Dahan, A.B. Martin, D.S. Chemia, P.E. Dawson, P.G. Schultz, and S. Weiss. ”Single-molecule protein folding: diffusion fluorescence energy transfer studies of the denaturation of chymotrypsin inhibitor 2.” Proc.Natl.Acad.Sci. USA 97(2000):5197-5184.
[57] Pons, Thomas. ”Single-Molecule Applications.” In FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 323-356. Weinheim Germany: Wiley-VCH, 2014.
6 Further Reading
General FRET:
FRET - Förster Resonance Energy Transfer From Theory to Applications edited by Igor Medintz and Niko Hildebrandt, 23-62. Weinheim Germany: Wiley-VCH, 2014.
On the history of FRET: Reference 4: Clegg, Robert M. “The History of FRET.“ In Reviews in Fluorescence, volume 3, edited by C.D. Geddes and J.R. Lakowicz, 1-45. Springer International Publishing Switzerland 2014. Reference 8: Masters, B.R. “Paths to Förster’s resonance energy transfer (FRET) theory.” Eur. Phys. J. H. 39(2014): 87-139, DOI: 10.1140/epjh/e2013-40007-9
Unified theory describing both radiative and radiationless transfer using a single excitation transfer function constructed using Quantum Electro Dynamics: Andrews, D.L. “A unified Theory of Radiativ and Radiationless Molecular Energy Transfer”, Chemical Physics 135(1989): 195-201, https://ueaeprints.uea.ac.uk/56540/1/050.pdf