Bouguer-Lambert-Beer Absorption Law
Leif Gerward
Department of Physics, Technical University of Denmark, DK-2800 Lyngby/Denmark.
1 Introduction
It is well known that the intensity [math]I[/math] of light (or other electromagnetic radiation) should decrease exponentially with the distance d that it enters an absorbing medium, i.e. [math]I=I_{0}exp(-\mu d)\tag {1}[/math] where [math]I_{0}[/math] is the intensity of the incident radiation, and μ is the linear absorption (or attenuation) coefficient. Equation (1) is usually known as Lambert’s law of absorption (e.g. Ballentyne and Lovett, 1970). However, there is some confusion about the origin of that law, since other names are Lambert–Beer’s law and Bouguer’s law. Therefore, it should be interesting to know a little more about the scientists associated with the Absorption Law, and about their contributions to the subject. As it turns out, the story has already been told. Fred Perrin (1948) has published a note with the somewhat provocative title “Whose Absorption Law?” Perrin’s paper, however, appeared almost sixty years ago, and few may be aware of it today. Thus, for the benefit of the reader of the Bulletin, it should be worthwhile once again to discuss the origin of the Absorption Law. I have also extended the scope of the present paper by including biographical sketches of Bouguer, Lambert and Beer.
2 Pierre Bouguer (1698–1758)
Pierre Bouguer was a child prodigy trained by his father, Jean Bouguer, who was a professor of hydrography at Croisic in Lower Brittany, France. The father died when Pierre was 15 years old, but by then the son had already acquired enough knowledge in mathematics and natural sciences to succeed in the chair of his father. In spite of his young age, Pierre lectured with great authority on topics such as mathematics, physics and astronomy. The French Académie des Sciences awarded him several prizes for his work, and in 1731 he became himself a member of the Academy. In 1735 he participated in an expedition to Peru to measure the length of a degree of meridian at the equator (this expedition was part of a larger project aimed at determining the shape of the Earth). Bouguer also measured gravity at different altitudes and was the first to estimate the gravitational pull of mountains, the so-called Bouguer correction.
Pierre Bouguer (Fig. 1) devoted most of his professional life to the solving of nautical problems. However, he is also known as the father of photometry. In 1729 he published an extensive work, Essai d’optique sur la gradation de la lumière, where he laid the foundation of this branch of science. In the present context it is interesting to note that Bouguer, among other things, investigated the absorption of light in the atmosphere and other transparent media. Bouguer’s optical work was posthumously published in 1760 as Traité d’optique sur la gradation de la lumière.
Chapter two of the Essai d’optique deals with transparency and opacity of matter. Bouguer takes the trouble to explain in detail how the intensity of light decreases upon traversing a transparent body. In his model, the body is divided into a number of layers of equal thickness, and the light rays are incident perpendicular to the layers. At first sight, one might think that the intensity of light should decrease in arithmetical progression, but Bouguer argues that this cannot be true. Instead, as he correctly points out, the intensity will always decrease in geometrical progression, since each layer absorbs a constant fraction of the intensity incident upon it. Therefore,
- the intensity of light, after traversing different thicknesses, can be represented by the ordinates of a logarithmic [curve], which has the thickness of the medium as its axis [of abscissae] (Bouguer, 1729).
As noticed by Bouguer, the logarithmic curve, which is well known to mathematicians and surveyors, has the properties that the subtangent is constant and, most importantly in the present case, the ordinates decrease in geometrical progression.
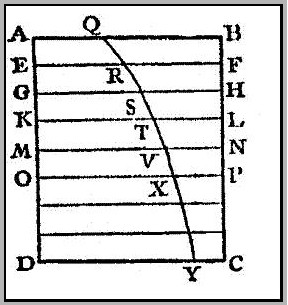
In order to illustrate his point, Bouguer considers a perfectly homogenous body ABCD, divided into layers of equal thickness (Fig. 2). The light is incident perpendicular to the face AB. The length QB represents the incident intensity. After having traversed the depth BF or AE, the light enters the second layer through the face EF. At this depth the intensity is RF. In this way, the intensity as a function of depth can be described by the logarithmic curve QRXY, where BC is the axis of abscissae (the x-axis). For a less transparent body the intensity will decrease more rapidly. In fact, the shape of the transmission curve is determined solely by its subtangent and by the intensity of the incident radiation. Bouguer then goes on, giving several examples of how transmission curves can be constructed and used in various problems.
It follows from above that Bouguer has given a correct description and interpretation of the transmission of light in a transparent body, although he has not expressed the Absorption Law in the concise form of Equation (1), later to be derived by Lambert.
3 Johann Heinrich Lambert (1728–1777)
Johann Heinrich Lambert was an autodidact, who had to rely on his own efforts for his education. Son of a poor tailor in Mühlhausen, Elsass (Alsace), he had to leave school at the age of twelve to help his father with tailoring. At the age of fifteen he worked as a clerk at the nearby ironworks to earn money for the family. Two years later, he took up a position as secretary to Professor Iselin, the editor of a newspaper at Basel, Switzerland. Lambert could now use his spare time for studies in natural sciences and philosophy.
In 1748, Iselin recommended the young Lambert for a position as private tutor in the home of Count Peter von Salis, who lived in Chur, Switzerland. Here, Lambert got access to the excellent library of the Count, and he seized the opportunity to delve deeply into mathematics, astronomy and philosophy. While in Chur, Lambert first came to be noticed by the scientific community of his time. He made his own astronomical instruments, and he began to publish articles in scientific journals. In 1756 Lambert left Chur with two of the older boys he had tutored during the previous eight years. Lambert and the two young men made a “grand tour” of Europe, of two years duration, visiting several cities and scientific centres, such as Göttingen, Utrecht, Paris, Marseilles and Turin.
Soon after the grand tour, the thirty years old Lambert resigned his tutorship and settled for a while in Augsburg, Germany. Subsequently, Munich, Erlangen, Chur and Leipzig became for brief intervals his home in search for a scientific position. Finally, in 1764, he got a call to join the Berlin Academy of Sciences, founded by Frederick the Great of Prussia. Director of the Berlin Academy was the famous Swiss mathematician Leonhard Euler, who in 1766 was succeeded by the equally famous Italian-French mathematician Joseph Louis Lagrange.
Lambert (Fig. 3) was a prolific writer. As a member of the Prussian Academy for twelve years, until his death at the age of forty-nine, he produced more than 150 works for publication. He was recognized as one of the best mathematicians of his day. For example, he provided the first rigorous proof that the number pi is irrational, and he made the first systematic development of hyperbolic functions. Lambert made many innovations in the study of heat and light, and several physical laws and units are named after him. In 1760 he published his great work on photometry, Photometria sive de mensura et gradibus luminus, colorum et umbrae. Lambert also made a major contribution to philosophy, and he corresponded with the German philosopher and cosmologist Immanuel Kant.
Lambert successfully found functional equations by expressing physical properties in the language of the differential calculus. Thus, he was first to express Newton’s second law of motion in the notation of differential calculus and, most interestingly in the present context, he derived the Absorption Law in the concise form of Equation (1).
In his Photometria, Lambert derives the Absorption Law in much the same way as can be seen in modern textbooks. He considers a differential layer with thickness [math]dx[/math] at distance x into the absorbing body. He then assumes that the fractional reduction of the beam intensity, [math]–dI/I[/math], is proportional to the density of the medium and the layer thickness [math]dx[/math], and he arrives at the following differential equation: [math]-dI=\mu Idx\tag {2}[/math] where the linear attenuation coefficient [math]\mu[/math] is proportional to the density of mass, [math]\rho[/math] (modern data tabulations are usually in terms of the mass attenuation coefficient, [math]\mu/\rho[/math]). For simplicity, I am here using the modern notation, although Lambert uses a slightly different notation in his original paper. Integrating Equation (2), one obtains the intensity after traversing the distance d into the absorbing body [math]\ln \left ( I_{0}/I \right )=\int_{0}^{d}\mu dx\tag{3}[/math] For a homogenous medium, Equation (3) reduces to [math]\ln \left ( I_{0}/I \right )=\mu d\tag{4}[/math] from which the exponential absorption law of Equation (1) follows.
4 August Beer (1825–1863)
August Beer appears to have had a smooth career. He was born in Trier, Germany, where he studied mathematics and natural sciences. He continued, working for the mathematician and physicist Julius Plücker (who in 1857 discovered the cathode rays) in Bonn, and obtained his doctorate in 1848. Two years later, he was appointed professor of mathematics and physics at the University of Bonn. In 1854, he published a book on optics, “Einleitung in die höhere Optik”.
In 1852, Beer published a paper on the absorption of red light in coloured aqueous solutions of various salts. Beer makes use of the fact, derived from Bouguer’s and Lambert’s absorption laws, that the intensity of light transmitted through a solution at a given wavelength decreases exponentially with the path length [math]d[/math] and the concentration [math]c[/math] of the solute (the solvent is considered non-absorbing). Actually, the “Absorption Coëfficient” defined by Beer in his paper is the transmittance (or transmission ratio),[math]T=I/I_{0}[/math]. Thus, as pointed out by Beer,
- the transmittance of a concentrated solution can be derived from a measurement of the transmittance of a dilute solution (Beer, 1852).
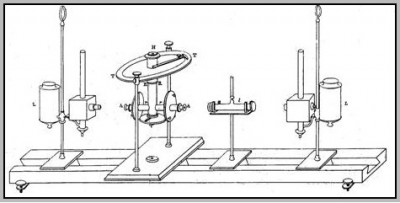
Indeed, the transmittance measured for any concentration and path length can be normalized to the corresponding transmittance for a standard concentration and path length. Beer in a number of experiments confirms this, defining a standard concentration of 10%, and a standard path length of 10cm. The photometer, devised by Beer, is shown in Fig. 4. Explicitly, Beer’s absorption law for a solute in a non-absorbing solvent can be expressed as [math]A=\ln \frac{I_{0}}{I}=\varepsilon' c d\tag{5}[/math] where [math]A[/math] is the absorbance (formerly, and still widely, the optical density) and [math]\varepsilon[/math] is the molar absorption coefficient (formerly the extinction coefficient). The molar absorption coefficient [math]\varepsilon[/math] is normally expressed in units of [math]L mol^{-1}cm^{-1}[/math]. Alternative units are [math]cm^{2}mol^{-1}[/math]. This change of units emphasizes the point that [math]\varepsilon[/math] is a molar cross section for absorption.
In spectroscopy and spectrometry it is common practice to convert the logarithm to base 10. Using the relation [math]\ln x=\ln 10\times \log x[/math], it is easy to show that Beer’s law can be expressed as [math]A=\log \frac{I_{0}}{I}=\varepsilon c d\tag{6}[/math] where the molar absorption coefficient [math]\varepsilon[/math] is given by [math]\varepsilon=\varepsilon'ln10=2.30258509299\varepsilon'.\tag{7}[/math] In passing, it may be mentioned that Beer’s law also can be applied to gaseous mixtures, for example the atmosphere. The concentration of each constituent gas is then usually expressed in terms of its partial pressure.
5 Conclusions
In some sense it is appropriate to name the Absorption Law after Lambert, since he was first to derive Equation (1) in its concise form using differential calculus. However, one should remember that in principle Bouguer has priority, since he was first to describe the transmission of light in a transparent body in terms of the logarithmic curve. The notation Beer’s Law, on the other hand, should be reserved for Equations (5) and (6), describing the special case of attenuation of light (or other electromagnetic radiation) in a solution. The present author once remarked that
- if measurements of attenuation coefficients of solutions become common practice, it might be useful to quote the atomic cross sections in units of cm2/mol instead of the presently accepted units of b/atom or b/molecule (Gerward, 1996).
If so, Lambert’s Law and Beer’s Law would merge into a single Absorption Law.
6 Acknowledgment
I wish to thank John H. Hubbell for kindly copying the papers by Bouguer and Lambert from his file.
7 References
D.W. Ballentyne and D.R. Lovett, A Dictionary of Named Effects and Laws in Chemistry, Physics, and Mathematics, 3rd Ed. Chapman and Hall Ltd., London 1970, p. 188.
A. Beer, Bestimmung der Absorption des rothen Lichts in farbigen Flüssigkeiten. Annal. Phys. Chem. 86 (1852) 78–88.
P. Bouguer, Essai d’optique sur la gradation de la lumière. Gauthier-Villars et Cie, Paris 1729 (reprinted in 1929 with a Biographic note and a Preface).
L. Gerward, On the attenuation of X-rays and gamma rays in dilute solutions. Radiat. Phys. Chem. 48 (1996) 697–699.
J.H. Lambert, Photometria sive de mensura et gradibus luminus, colorum et umbrae (1760). Published in German by E. Anding under the title Lambert’s Photometrie, Verlag von Wilhelm Engelmann, Leipzig 1892.
F.H. Perrin, Whose Absorption Law? Opt. Soc. Am. 38 (1948) 72–74.