Large Excitation Energy Transfer Dynamics in Nano-Hybrid Systems
by Dirk Ziemann, Thomas Plehn and Volkhard May
Institut für Physik, Humboldt-Universität zu Berlin, Newtonstraße 15, D-12489 Berlin, Germany, EU
1 Introduction
Electronic excitation energy transfer (EET) represents an ubiquitous phenomenon in physical chemistry, nanophotonics, plasmonics and other disciplines of nanoscience. It interrelates quantum system [math]1[/math] with ground state [math]|1g\rangle[/math] and excited state [math]|1e\rangle[/math] to quantum system [math]2[/math] with ground state [math]|2\bar{g}\rangle[/math] and excited state [math]|2\bar{e}\rangle[/math] via the energy exchange matrix element [math]V_{\rm EET}=\langle 2\bar{e}|\langle 1g|\hat{W}|1e\rangle|2\bar{g}\rangle[/math][1]. The complete Coulomb-interaction (electrostatic interaction) among the charges of system 1 and system 2 (electrons and nuclei) is denoted by [math]\hat{W}[/math]. The formula assumes vanishing wave function overlap between both systems. Thus charge (particle) exchange contributions do not appear. Besides a sufficiently large [math]V_{\rm EET}[/math] a further supposition for efficient EET is that the excitation energy [math]E_{1 e} - E_{1 g}[/math] of the one system is comparable with the excitation energy [math]E_{2 \bar e} - E_{2 \bar g}[/math] of the other system. We also emphasize that this type of EET can be understood as the short distance version of a general quantum electrodynamic photon exchange process (see, for example, [1]).
The variant of EET which refers to molecules is connected with the name of Förster. Respective rates display the famous [math]\frac{1}{R^{6}}[/math]- dependence ([math]R[/math] denotes the intermolecular distance) since the coupling is dominated by molecular electronic transition point dipoles. If the charge distribution in the interacting species is more complex the [math]\frac{1}{R^{6}}[/math]- dependence of the rate undergoes drastic changes. This can be demonstrated, for example, by combining nano-systems of varying composition and shape [2, 3]. The coupling of molecules to differently shaped semiconductor nano-crystals (NCs) was of particular interest in this respect (c.f., for example [4] - [10]). In contrast to the extended experimental work, theoretical studies describing molecule-NC EET with an atomistic resolution found less interest. A dipyridyl porphyrin interacting with a Cd[math]_{33}[/math] Te[math]_{33}[/math] NC coated by a Zn[math]_{78}[/math]S[math]_{78}[/math] shell has been investigated in [11] using a DFT approach. In Ref. [12] EET rates for a CdSe-NC chlorophyll complex were determined. TD-DFT techniques could be applied in [13] to a tiny Cd[math]_{6}[/math]Te[math]_{6}[/math] cluster interacting with a rhodamin cation. In a similar way EET among different NCs was investigated [14]. More recent work concentrated on EET at the interface of a molecular layer and a ZnO slab [15, 16].
It is the intention of the subsequent discussion to review our own theoretical work on EET between individual molecules or molecular systems (MS) and semiconducting NC [17, 18, 19]. Ref. [17] focused on EET between a CdSe NC and a single tetrapyrrole-type pheophorbide-[math]\it a [/math] molecule. In Ref. [18] we considered EET which may proceed between a huge cyanine dye complex and a CdSe nano-crystal. Recently we studied EET from a [math]\pi[/math]-stacked complex of [math]\it para[/math]-sexiphenyl (6P) molecules to a hemispherical ZnO NC [19]. Before presenting details of EET in these three different systems we give an introduction to the computation of molecular and NC electronic excitations, the determination of their mutual coupling, and the computation of EET rates.
2 Models of Nano-Hybrid Systems
2.1 Molecular Part
The MS shall be described by singly excited electronic states which may constitute Frenkel-like excitons. Those are the correct excitations if wave function overlap and thus electron exchange between different molecules are of minor effect. The related standard Hamiltonian reads
[math]H_{\rm FX} = \sum_{m} E_m |{\phi_m}\rangle\langle{\phi_m}| + \sum_{m \neq n} J_{m n} |{\phi_m}\rangle\langle{\phi_n}|.\tag{1}[/math]
It includes the molecular excitation energies (site energies) [math]E_{m}[/math] where [math]m[/math] labels the individual molecule and the EET (excitonic) coupling [math]J_{m n}[/math]. The [math]\phi_{m}[/math] are molecular product states with molecule [math]m[/math] in the first excited state [math]\varphi_{m e}[/math] and all other molecules in the ground-state [math]\varphi_{n g}[/math]:
[math]|{\phi_m}\rangle = |{\varphi_{m e}}\rangle \prod_{n \neq m} |{\varphi_{n g}} \rangle.\tag{2}[/math]
The site energies [math]E_{m}[/math] are in the simplest version given by the difference of the excited state energy [math]E_{m e}[/math] and the ground-state energy [math]E_{m g}[/math]. The overall ground-state is
[math]|{\phi_0}\rangle = \prod_m |{\varphi_{m g}}\rangle.\tag{3}[/math]
The ground-state part [math]E_0 |{\phi_0}\rangle\langle{\phi_0}|[/math] does not appear in the Hamiltonian since we set the respective energy equal to zero. The excitonic coupling [math]J_{m n}[/math] coincides with [math]J_{m n}(e g, e g)[/math] what is a particular example of the general two-molecule Coulomb matrix element [1]
[math]J_{m n}(a b, b' a') = \int d^3 {\bf x} \; d^3 {\bf y} \; \frac{n^{(m)}_{a a'}({\bf x}) n^{(n)}_{b b'}({\bf y})}{|{\bf x} - {\bf y}|} \tag{4}.[/math]
It appears as the Coulomb interaction of the charge density [math]n^{(m)}_{a a'}(\mathbf{x})[/math] of molecule [math]m[/math] represented by electronic state index [math]a[/math] and [math]a'[/math] as well as the charge density [math]n^{(n)}_{b b'}(\mathbf{y})[/math] of molecule [math]n[/math] represented by electronic state index [math]b[/math] and [math]b'[/math]. The molecular charge density takes the form
[math]n^{(m)}_{a a'}({\bf x}) = \rho^{(m)}_{a a'}({\bf x}) - \delta_{a, a'} r^{(m)}_a ({\bf x})\tag{5}. [/math]
If [math]a \neq a'[/math] it is exclusively determined by the electronic transition density [math]\rho^{(m)}_{a a'}({\bf x})[/math]. If [math]a = a'[/math], it is corrected by the nuclear charge density (plus core electrons) [math]r^{(m)}_a ({\bf x})[/math] concentrated at the atomic positions [1]. For concrete computations the continuous charge densities are replaced by discrete atomic centered partial charges and partial transition charges [20]. Single exciton states as eigenstates of [math]H_{\rm FX}[/math], Eq. (1), are of the form
[math]|{\alpha}\rangle = \sum\limits_m C_\alpha(m) |{\phi_m}\rangle\tag{6}.[/math]
The related energy is denoted by [math]E_\alpha[/math]. We briefly describe possible generalizations of this definition of Frenkel-like excitons (see Ref. [18]). In order to do this we note that the Frenkel-like exciton Hamiltonian, Eq. (1), appears as the singly excited state part of the complete MS Hamiltonian [1, 21]. The latter can be written as
[math]H_{\rm MS} = \sum_m H_m + \frac{1}{2} \sum_{m, n} V_{m n} \tag{7},[/math]
where [math]H_m[/math] is the single molecule Hamiltonian. The coupling [math]V_{m n}[/math] accounts for all types of Coulomb-interactions between molecule [math]m[/math] and [math]n[/math]. To distinguish between singly and multifold excited states we introduce general product states
[math]|{A}\rangle = \prod_m |{\varphi_{m a}}\rangle \tag{8}.[/math]
Every molecule may be placed in an arbitrary excited state [math]\varphi_{m a}[/math]. When calculating matrix elements of [math]H_{\rm MS}[/math] with singly excited states one arrives at [math]H_{\rm FX}[/math], Eq. (1), but including electrostatic couplings due to permanent charge distributions in the ground and the excited state of the molecules. It results in the shifts
[math]\Delta E_m = \sum_k [J_{m k}(e g, g e) - J_{m k}(g g, g g)]\tag{9}[/math]
of site-energies [math]E_m[/math]. Moreover, there appear couplings to higher excited states [math]|{A}\rangle[/math] which introduces polarization effects and changes somewhat further the [math]E_m[/math] and [math]J_{m n}[/math] [22, 23]. This indicates that the exclusive use of singly excited states [math]|{\phi_m}\rangle[/math] to define Frenkel-like excitons is only an approximate approach. Such a situation is standard in quantum chemistry where the computation of a singly excited electronic state by single excited configurations offers only a rough approximation (configuration interaction approach reduced to a single type of configurations - CIS).
2.2 Nano-Crystal Part
To compute singly excited electron-hole pair states of large NCs with some thousands of atoms we combined a semiempirical tight-binding description of the individual electron and hole states with a consideration of the Coulomb-attraction in a CI methodology [24-29]. Tight-binding states of the NC are defined as [17]
[math]|{\psi_a({\bf r})}\rangle = \sum_s \psi_a({\bf r}, s) |{s}\rangle.\tag{10}[/math]
The expression includes the consideration of spin-orbit coupling. The spin quantum number [math]s[/math] enters the single electron wave function
[math]\psi_a({\bf r}, s) =\sum_{u, o} A_a(u o s) \xi_{u o}({\bf r}).\tag{11}[/math]
Atomic orbitals [math]\xi_{u o}[/math] are labeled by the atom index [math]u[/math] and the orbital index [math]o[/math]. It result delocalized single-particle states with quantum number [math]a[/math]. Respective energies belong to occupied states (at [math]T = 0[/math]) in the valence-band-like part of the spectrum or to unoccupied states in the conduction-band-like part of the spectrum. The empty states are the electron states with energy [math]E_a[/math]. If occupied states get unoccupied a hole state is formed with energy [math]E_{\bar a}[/math]. Accordingly, the energy of an electron-hole pair is [math]E_a - E_{\bar a}[/math]. We set the energy of the filled valence-band-like states equal to zero and get the electron-hole Hamiltonian according to
[math]H_{\rm WX} = \sum_a E_a e^+_a e_a - \sum_{\bar a} E_{\bar a} h^+_{\bar a}h_{\bar a} - \sum\limits_{a, b} \sum\limits_{{\bar a}, {\bar b}}\big( W^{\rm (e-h)}_{a {\bar a}, {\bar b} b} - J^{\rm (e-h)}_{a {\bar a}, {\bar b} b} \big)e^+_a h^+_{\bar a} h_{\bar b} e_b.\tag{12}[/math]
Electrons are represented by the second quantization operators [math]e^+_a[/math] and [math]e_b[/math]. For the holes we introduced [math]h^+_{\bar a}[/math] as well as [math]h_{\bar b}[/math]. The electron-hole pair interaction is constituted by two contributions, where the Coulomb part reads
[math]W^{(e-h)}_{a {\bar a}, {\bar b} b} = \int\limits d^3 {\bf x} \; d^3 {\bf y} \; \frac{\rho_{a b}({\bf x}) \rho^*_{{\bar a} {\bar b}}({\bf y})}{ |{\bf x} - {\bf y}|}.\tag{13}[/math]
We introduced the electron-electron transition charge density
[math]\rho_{a b}({\bf x}) = e \sum\limits_s \psi^*_a({\bf x}, s) \psi_{b}({\bf x}, s)\tag{14},[/math]
and the hole-hole transition charge density
[math]\rho_{{\bar a} {\bar b}}({\bf y}) = e \sum\limits_{\bar s} \psi^*_{{\bar a}}({\bf y}, {\bar s}) \psi_{\bar b}({\bf y}, {\bar s}). \tag{15}[/math]
Accordingly, the Coulomb part corresponds to processes where an electron is scattered at a hole (and vice versa). The exchange part takes the form
[math]J^{(e-h)}_{a {\bar a}, {\bar b} b} = \int\limits d^3 {\bf x} \; d^3 {\bf y} \; \frac{\rho_{a {\bar a}}({\bf x}) \rho^*_{b {\bar b}}({\bf y})}{ |{\bf x} - {\bf y}|} \tag{16}.[/math]
It covers the electron-hole transition charge densities of type
[math]\rho_{a {\bar a}}({\bf x}) = e \sum\limits_s \psi^*_a ({\bf x}, s) \psi_{\bar a}({\bf x}, s) \tag{17},[/math]
and determines processes where the electron-hole pair in the states [math]\psi_b \psi^*_{\bar b}[/math] is annihilated and, afterwards, an electron-hole pair in the states [math]\psi_a \psi^*_{\bar a}[/math] is created. This is identical with the way molecular excitation energy is transferred from one molecule to another.
The single Wannier-Mott-like exciton states with energy [math]E_\gamma[/math] can be introduced as
[math]|{\psi_\gamma}\rangle = \sum\limits_{a, {\bar a}} C_{\alpha}(a {\bar a}) e^+_a h^+_{\bar a} |{\psi_0}\rangle \tag{18}.[/math]
However, be aware of the fact that the present approach does not account for two or more electron-hole pair excitations since electron-electron and hole-hole Coulomb-interaction have been neglected.
2.3 EET Coupling Between the Molecular and the Nano-Crystal Part and Rates of EET
The EET coupling which describes MS de-excitation and NC excitation generally reads
[math]V_{\gamma \alpha} = \langle{\psi_\gamma}|\langle{\phi_g}|\sum_{j, j'} \frac{e^2}{|{\bf x}_j - {\bf y}_{j'}|}|{\alpha}\rangle|{\psi_0}\rangle\tag{19}.[/math]
The expression is responsible for a transition from the product state with an excited MS [math]|{\alpha}\rangle|{\psi_0}\rangle[/math] to the excited NC state [math]|{\phi_g}\rangle|{\psi_\gamma}\rangle[/math] ([math]|{\phi_g}\rangle[/math] is the ground-state of the MS and [math]|{\psi_0}\rangle[/math] is that of the NC). The two types of product states are connected to each other by the Coulomb-coupling between all electrons of the MS and all electrons of the NC. As in similar cases the matrix elements can be reduced to a simple Coulomb-interaction among single particle like densities
[math]V_{\gamma \alpha} = \int d^3 {\bf x} \; d^3 {\bf y} \; \frac{\rho_\gamma({\bf x}) \rho^*_\alpha({\bf y})}{ |{\bf x} - {\bf y}|} \tag{20}.[/math]
The NC exciton transition density reads
[math]\rho_{\gamma}({\bf x}) = \sum_{a, {\bar a}} C_{\gamma}(a {\bar a}) \rho_{a {\bar a}}({\bf x}) \tag{21},[/math]
with the electron-hole transition density[math]\rho_{a {\bar a}}({\bf x})[/math] already defined in Eq.(17). Its discretization results in atomic centered transition charges referring to the different exciton levels. For the Frenkel-like exciton transition density we get
[math]\rho_\alpha({\bf y}) = \sum_m C_\alpha(m) \rho^{(m)}_{e g}({\bf y}) \tag{22}.[/math]
The single molecule transition density has been already introduced in Eq. (5). We may also write
[math]V_{\gamma \alpha} = \sum_{a, {\bar a}} \sum_m C_{\gamma}(a {\bar a}) C^*_\alpha(m) V_{a{\bar a}, m}\tag{23}[/math]
with
[math]V_{a {\bar a}, m} = \int d^3 {\bf x} \; d^3 {\bf y} \; \frac{\rho_{a {\bar a}}({\bf x})\rho^*_m({\bf y})}{ |{\bf x} - {\bf y}|} \tag{24}.[/math]
The expression highlights the influence of the spatial distribution of the molecular excitations in the Frenkel-like exciton and the electron-hole pair distribution in the Wannier-Mott-like exciton. If the respective wave function are free of nodes the individual MS and NC contributions add to each other. Cancelation appears if nodes are present.
EET from the MS to the NC has to be described by the following rate
[math]k_{\rm MS \to NC} = \frac{2 \pi}{\hbar} \sum_{\alpha, \gamma}f_\alpha |V_{\gamma \alpha}|^2 \delta(E_\alpha - E_\gamma) \tag{25}.[/math]
The rate for the reverse process reads
[math]k_{\rm NC \to MS} = \frac{2 \pi}{\hbar} \sum_{\gamma, \alpha}f_\gamma |V_{\gamma \alpha}|^2 \delta(E_\gamma - E_\alpha) \tag{26}.[/math]
The MS to NC transfer takes place from a thermal distribution [math]f_\alpha = 1 / Z \times \exp (- E_\alpha/k_{\rm B} T)[/math] of Frenkel-like excitons. For the reverse process, the transfer starts from a thermal distribution [math]f_\gamma[/math] of Wannier-Mott-like excitons. Usually one accounts for vibrational effects by a life-time broadening of the [math]\delta[/math]-function according to [math]\Gamma / \pi \times 1/([E_\alpha - E_{\bar \alpha}]^2 + \Gamma^2)[/math]. If the NC is not too small (3000 to 4000 atoms or more) the Wannier-Mott-like exciton levels at a somewhat higher part of the spectrum form a quasi-continuum and the concrete value of [math]\Gamma[/math] is not so essential.
3 The Pheophorbid-a CdSe-NC System
As a first example for EET in nano-hybrid systems we consider the transfer from a CdSe NC to the tetrapyrrole type Pheophorbide-a molecule (Pheo; cf. Fig. 1 and Ref. [17]). The rate expression accounts for the correct NC-Pheo transfer coupling, for the multitude of NC single exciton levels as well as their thermal distribution, and for the electron-vibrational Pheo states. Accordingly, Eq. (26) is modified to
[math]k_{\rm NC \to MS} = \frac{2 \pi}{\hbar} \sum_\alpha f_\alpha |V_{e 0, \alpha g}|^2 {\cal D}_{g \to e}(E_\alpha)\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;,(27)[/math]

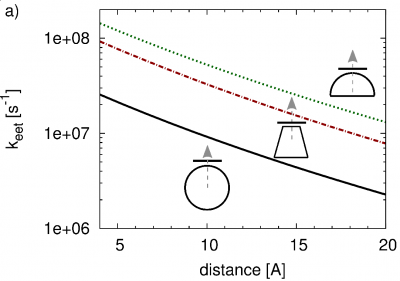
where [math]{\cal D}_{g \to e}[/math] denotes the combined DOS of the ground-state excited state transition in Pheo (see also Fig. 2 and for details Ref. [17]). NC-exciton levels are computed in the framework of the described tight-binding approach combined with a CI-characterization of the Coulomb correlated electron-hole pairs. State of the art DFT and TD-DFT methodologies are utilized for a description of Pheo, whose first excited state (so-called Q[math]_y[/math]-excitation) fits well to the fundamental single exciton of CdSe NCs (concerning necessary data we refer to Ref. [30]). A particular aspect of the investigation was the comparison of three types of CdSe NCs (see the insert in the left panel of Fig. 3). We consider a spherical Cd[math]_{1159}[/math]Se[math]_{1450}[/math] NC (s-NC, diameter of [math]5.2[/math] nm), a Cd[math]_{1156}[/math]Se[math]_{1418}[/math] NC given by a hemisphere (h-NC, diameter of [math]6.0[/math] nm), and a Cd[math]_{1180}[/math]Se[math]_{1449}[/math] NC of pyramidal shape (p-NC, base length of [math]6.0[/math] nm and height of [math]3.2[/math] nm).
The NC-molecule transition rate, Eq. (27), notices the thermal distribution of NC-excitons. Accordingly, the lowest exciton states are of interest only. To obtain reliable values for the respective energies, up to 6800 electron-hole configurations for every type of NC were included in the calculations. Due to the different energetic distribution of electron and hole levels we took into consideration 40 electron states and 170 hole states (for the p-NC 38 electron and 176 hole states). Here and for further use the Wannier-Mott-like exciton energies are written as
[math]E_\alpha = E_X + \Delta E_\alpha \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;,(28)[/math]
where [math]E_X[/math] is the lowest exciton energy. The [math]\Delta E_\alpha[/math] are displayed in Fig. 2 for the three types of NCs.
For the s-NC the Coulomb coupling results in a 181 meV shift of [math]{\cal E}_X[/math] below the fundamental energy gap [math]{\cal E}^{\rm (s-NC)}_g = 2.125[/math] eV. The shift amounts to 179 meV for the h-NC and p-NC ([math]{\cal E}^{\rm (h-NC)}_g = 2.105[/math] eV and [math]{\cal E}^{\rm (p-NC)}_g = 2.111[/math] eV). The 80 meV energy window chosen in Fig. 2 covers the energy range where thermalized excitons (at room temperature) contribute to the rate.
Interestingly, the energetic distance between the lowest pair of levels and the successive pair is similar for all types of NCs (it results from the exchange coupling between the single particle states). In contrast, the energetically higher part of the exciton spectrum displays pronounced differences between the s-NC and the two other NCs. Concerning the s-NC there are 16 exciton states up to [math]\Delta {\cal E}_X = 50[/math] meV. In the same energy range, the h-NC as well as the p-NC only realize eight exciton states. Hence, a larger number of exciton states of the s-NC contributes to the EET. The exciton spectra of the h-NC and p-NC are similar for [math]\Delta {\cal E}_X\lt50[/math] meV but show differences above this value (the similarity in the shape of the p-NC and h-NC leads to some similarities of the exciton spectrum).
The presentation of the EET couplings [math]V_{e 0, \alpha g}[/math] together with the Pheo DOS versus [math]\Delta E_\alpha[/math] in Fig. 2 offers a first impression on the magnitude of the transition rate [math]k_{\rm NC \to MS}[/math], Eq. (27). We expect the largest one for the p-NC and the h-NC, because of their large coupling strength related to the lowest exciton states. Furthermore, there are additional differences with respect to the energies [math]E_X[/math] of the lowest exciton states. [math]E_X[/math] belonging to the h-NC is poistioned 49 meV above the molecular transition energy [math]E_{e g} + S_{e g}/2[/math]. In the case of the p-NC and s-NC the difference amounts to 54 meV and 57 meV, respectively. Obviously, a decrease of these energy differences results in an increase of [math]{\cal D}_{g \to e}(E_\alpha)[/math] and thus of the EET rate. Consequently, the largest rate should correspond to the h-NC, followed closely by the p-NC. The smallest rate shall belong to the s-NC. Fig. 3 confirms all this. Assuming the resonant case [math]E_X = E_{e g} + S_{e g}/2[/math] an increase of the rate by about one order of magnitude would be obtained. This may be realized by further increasing the size of the NC.
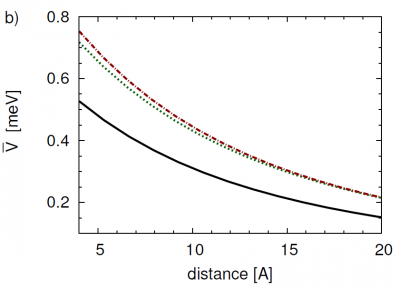
The introduced thermal averaged transfer coupling offers a single number to characterize all the various exciton levels and c
couplings
[math]{\bar V}^2 = \sum_\alpha f_\alpha |V_{e 0, \alpha g}|^2 \tag{29}.[/math]
According to Fig. 3, panel (a), [math]{\bar V}[/math] stays in the sub-meV-range for realistic Pheo NC distances. With respect to the formation of Pheo-NC hybrid states, this coupling regime has to be characterized as the weak-coupling one. Hybrid exciton formation would be impossible.
4 The Cyanin Dye Aggregate CdSe-NC System

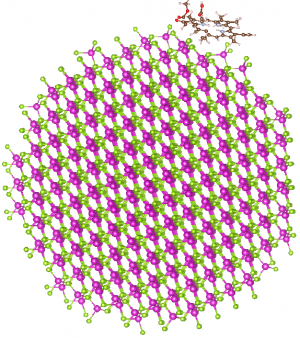
In the next example of EET in a nano-hybrid system we consider a huge tubular dye aggregate (TDA) and a CdSe-NC (see Fig. 4). Instead of a single molecular excitation as in the foregoing section the coupling is investigated of Frenkel-like exciton states of the TDA to Wannier-Mott-like excitations of the NC.
A double wall TDA of the cyanine dye C8S3 with a length of 63.4 nm and a diameter of 14.7 nm is considered. The TDA interacts with a spherical Cd[math]_{819}[/math]Se[math]_{630}[/math] NC of 4.5 nm diameter.
A recently repeated structure analysis of the TDA combined with extensive MD simulations resulted in a redefined spatial structure (it differs considerably from the one suggested in Ref. [31] and is described in detail in [22]). Accordingly, the TDA consists of six ribbons which are wrapped around a common axis to let the TDA be formed by an inner and an outer cylinder (see Fig. 4). Both cylinders have the same periodicity.
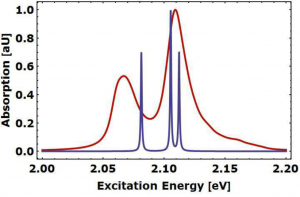
The Frenkel-like excitons of the TDA form a band with a width larger than 100 meV (see Figs. 5 and 6). It has been calculated for a finite TDA fragment of 63.4 nm length. According to the total number of 4140 C8S3 molecules the same number of exciton levels are considered (cf. also Fig. 4). The two main peaks in the absorption spectrum are originated by the inner and the outer wall, whose molecules undergo a somewhat different polarization shift [22].
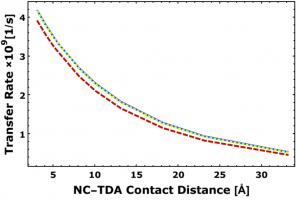
To discuss the EET rate we note Fig. 5, displaying the TDA and NC absorption spectrum and thus the main exciton levels. Fig. 6 also shows the EET coupling. A comparison indicates that the relevant NC-levels are all addressed by transitions from the TDA (the thermal distribution and the couplings [math]V_{\gamma \alpha}[/math] are large enough). Fig. 7 displays [math]k_{\rm MS \to NC}[/math], Eq. (25), versus the NC-TDA distance. This distance increases is realized by a NC-shift perpendicular to the TDA surface. Three different positions of the NC with respect to the TDA are chosen (NC in axial position and shifted away along the TDA). However, only the direct TDA-NC distance has an effect on the rate. Moving the NC perpendicularly away from the TDA decreases the rate. For the closest NC-TDA distance a life-time of the TDA excitation of about 250 ps is realized. This goes along with the observation that even in van der Waals contact the EET couplings between the exciton levels of the TDA and of the NC stay below 1 meV.
5 The Para-Sexiphenyl ZnO-NC System
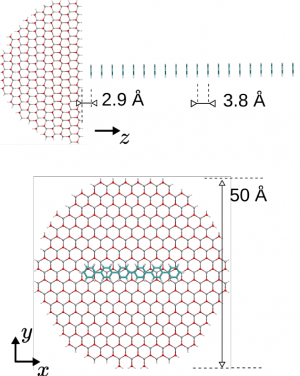
The third example of a nano-hybrid system where EET has been investigated is built up by a vertical stacking of 20 para-sexiphenyl (6P) molecules physisorbed on a ZnO NC (see Fig. 8). The NC is of hemispherical shape with 5 nm diameter and with 3903 atoms. We consider this as the best compromise between an essential nanoscopic scale to simulate a surface and the resulting numerical effort. The particular flat surface is terminated with Zn atoms to set up a (0001) slice. Corresponding to a physisorption process, the 6P molecules are arranged on top of this surface in van-der-Waals distance. Since the 6P transition dipole moments lie in the plane defined by the phenyl rings the molecular arrangement results in an H-aggregate type system. In combination and individually, both components have been extensively investigated in experiment and theory in the last few years [32-38].
We already studied charge separation dynamics in this type of system cf. [39, 40]. Here, different Frenkel-like exciton states of the 6P MS are chosen as excitation energy donor levels. In fact, experiments unveiled that the 6P HOMO-LUMO gap in molecular herringbone stacks attached to (0001) ZnO surfaces amounts to 3.5 eV [35]. Since the band gap of bulk ZnO of about 3.3 eV is smaller, EET into the manifold of semiconductor excitons also has to be expected for the present nano-hybrid system.
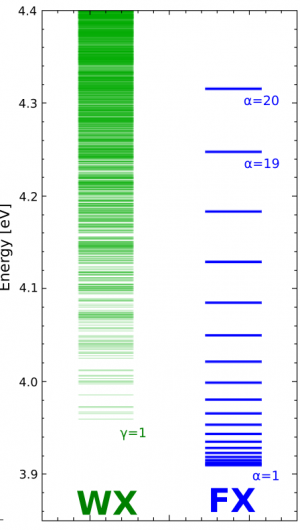
Fig. 9 displays the excited state energies of the organic and the inorganic part. The Frenkel-like exciton spectrum [math]E_\alpha[/math] of 20 levels covers the energy range from 3.91 up to 4.32 eV. We approximate the electronic excitations of the ZnO-system by uncorrelated electron-hole pairs. Respective CB-like and VB-like states and energies are computed within our tight-binding-model methodology and its recent extension to a DFTB approach. These ZnO excitations are also shown in Fig. 9. When going higher in energy the density of electron-hole pair excitations increases. The lowest excitation energy defining the ZnO band gap lies at 3.97 eV. Accordingly the lowest electron-hole pair energy is positioned within the Frenkel-like exciton band.
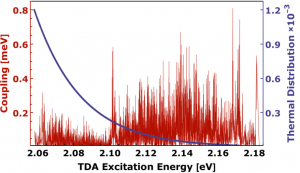
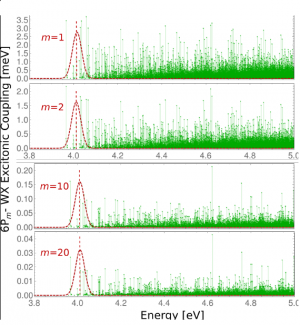
The EET coupling across the interface represents the central quantity for the present analysis. Before we will take a closer look at it, we will study the behavior of the quantity [math]V_{a {\bar a}, m}[/math], Eq. 24. It is responsible for EET from molecule [math]m[/math] to a particular ZnO electron-hole pair excitation. Fig. 10 displays this coupling versus the electron-hole pair energy, [math]E_a + E_{\bar a}[/math], and for different 6P molecules ([math]m = 1, 2, 10, 20[/math]). As it has to be expected the coupling strength decreases when changing from the 6P molecule close to the ZnO NC to the furthermost 6P. A certain variation of [math]V_{a {\bar a}, m}[/math] with the electron-hole pair energy is also obvious.
The situation is different if we turn to the Frenkel-like exciton electron-hole pair coupling
[math]V_{a {\bar a}, \alpha} = \sum_m C^*_\alpha (m) V_{a {\bar a}, m} \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;. (30)[/math]
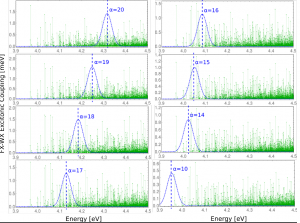
Fig. 11 displays this quantity for eight different exciton levels and versus the ZnO electron-hole pair energy. Most of the chosen exciton levels [math]E_\alpha[/math] are positioned away from the ZnO band gap energy. Therefore many electron-hole pair energies are close to the [math]E_\alpha[/math]. This justifies the above given neglect of Coulomb-correlation effects among the electron-hole pair excitations. Interestingly, all couplings lie in the 1-meV-region. However, the [math]\alpha =10[/math]-exciton is the lowest one which noticeable transfers energy to the ZnO system. All other excitons with [math]\alpha \lt 10[/math] are out of resonance and are ignored here.
When comparing the [math]V_{a {\bar a}, \alpha}[/math] with the coupling strength [math]V_{a {\bar a}, m}[/math], given in Fig. 10, one notices that the couplings of the upper Frenkel-like excitons are of about half the couplings to the two closest 6P molecules.
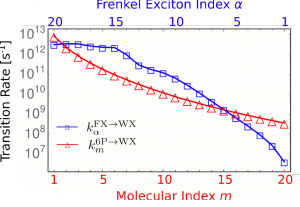
Transition rates are shown in Fig. 12 by drawing them versus the initial state quantum number (either [math]m[/math] or [math]\alpha[/math]). The largest values are about 10[math]^{12}[/math]/s, thus arriving at transfer times in the picosecond region. Since we consider uncorrelated electron-hole pairs as EET final states (energy acceptor) and a distinct Frenkel-like exciton as the energy donor we need to compute the rates
[math]k^{\rm FX \to WX}_\alpha = \frac{1}{2 \pi} \sum_{a, {\bar a}} |V_{a {\bar a}, \alpha}|^2 \delta(E_a + E_{\bar a} - E_\alpha) \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;. (31)[/math]
Besides, we will also analyze the transition from a single 6P molecule
[math]k^{\rm 6P \to WX}_m = \frac{1}{2 \pi} \sum_{a, {\bar a}} |V_{a {\bar a}, m}|^2 \delta(E_a + E_{\bar a} - E_m) \tag{32}.[/math]
Again the [math]\delta[/math]-functions are life-time broadened. Concerning the rates [math]k_{m}^{\rm{6P}\rightarrow\rm{WX}}[/math] we notice a particular distance dependence. It is mainly caused by the dependence of [math]V_{a {\bar a}, m}[/math] on the surface to 6P distance [math]d[/math] (the small change of the 6P excitation energy [math]E_m[/math] with [math]m[/math] is of minor influence). When increasing [math]d[/math] from the smallest value of 2.9Å to the largest value of 78.9Å (i.e. from [math]m=1[/math] to [math]m=20[/math]) the rate [math]k_{m}^{\rm{6P}\rightarrow\rm{WX}}[/math] dramatically decreases by four orders of magnitude (from [math]4.0\times 10^{12} {\rm s}^{-1}[/math] to [math]1.7\times 10^{8} {\rm s}^{-1}[/math]).
Next, we consider the rates [math]k_{\alpha}^{\rm{FX}\rightarrow\rm{WX}}[/math]. Those which belong to the upper part of the Frenkel-like exciton spectrum are as large as the largest EET rates which belong to the case where a single 6P donor molecule represents the initial state. This effect is valid down to [math]\alpha = 15[/math]. For lower levels we find a very rapidly decreasing rate.
In general, we may state that the EET from the upper Frenkel-like excitons is strongly assisted by the denser band of electron-hole pair EET acceptor states. Since this increase of the electron-hole pair DOS is usually the case our finding can be generalized to all H-aggregate like stackings.
6 Conclusions
Three examples of EET between a MS and a semiconducting NC have been presented. We discussed transfer (a) of Wannier-Mott-like excitations of a CdSe NCs to a pheophorbide-a molecule, from (b) Frenkel-like exciton states of a tubular dye aggregate formed by the cyanine dye C8S3 to a CdSe NC, and from (c) a vertical stacking of 20 para-sexiphenyl molecules to a hemispherical ZnO NC. Transition rates varied for closest MS-NC configurations between values of [math]10^8 {\rm s}^{-1}[/math] (case a), as well as values of some [math]10^9 {\rm s}^{-1}[/math] (case b) up to values of [math]10^{12} {\rm s}^{-1}[/math] (case c). However, the EET couplings stay in the 1 meV range or below. Accordingly, we only could demonstrate a weak-coupling-situation.
Formation of hybrid states between molecular and NC excitations, i.e. hybrid excitons are rather improbable. This is in contrast to the case where the semiconducting NC is replaced by a metal nano-particle. There, the same mechanism of EET coupling connects the molecular excitations with multipole plasmon excitations (for an overview see, for example [41]). However, the metal nano-particle plasmon transition densities are so large that the strong-coupling case is realized.
7 Acknowledgments
This work has been supported by the Deutsche Forschungsgemeinschaft through Sfb 951.
8 References
[1] May, V.; Kühn, O. Charge and Energy Transfer Dynamics in Molecular Systems; Wiley-VCH, Weinheim, 2000, 2004, 2011.
[2] Hernandez–Martinez, P. L.; Govorov, A. O.; Demir, H. V.; Generalized Theorey of Förster–Type Nonradiative Energy Transfer in Nanostructures with Mixed Dimensionality. J. Phys. Chem. C 2013, 117, 10203 – 10212.
[3] Hernandez-Martinez, P. L.; Govorov, A. O.; Demir, H. V. Förster-Type Nonradiative Energy Transfer for Assemblies of Arrayed Nanostructures: Confinement Dimension vs Stacking Dimension. J. Phys. Chem. C 2014, 118, 4951-4958.
[4] Alphandery, E.; Walsh, L.; Rakovich, Y. P.; Bradley, A. L.; Donegan, J. F.; Gaponik, N.; Gunko, Y. K. Highly Efficient Förster Resonance Energy Transfer Between CdTe Nanocrystals and Two Different Dye Molecules. Proc. SPIE 5462 2004, 87.
[5] Kloepfer, J. A.; Cohen, N.; Nadeau, J. L. FRET Between CdSe Quantum Dots in Lipid Vesicles and Water- and Lipid-Soluble Dyes. J. Phys. Chem. B 2004, 108, 17042-17049.
[6] Clapp, A. R.; Mednitz, I. L.; Mattoussi, H. Förster Resonance Energy Transfer Investigations Using Quantum-Dot Fluorophores. ChemPhysChem 2006, 7, 47- 57.
[7] Becker, K.; Lupton, J. M.; Müller, J.; Rogach, A. L.; Talapin, D. V.; Weller, H.; Feldmann, J. Electrical Control of Förster Energy Transfer. Nature Materials 2006, 5, 777-781.
[8] Sarkar, S.; Bose, R.; Jana, S.; Jana, N. R.; Pradhan, N. Doped Semiconductor Nanocrystals and Organic Dyes: An Efficient and Greener FRET System. J. Phys. Chem. Lett. 2010, 1, 636-640.
[9] Artemyev, M. Resonance Energy Transfer in Conjugates of Semiconductor Nanocrystals and Organic Dye Molecules. J. Nanophotonics 2012, 6, 061705.
[10] Dworak, L.; Matylitsky, V. V.; Ren, T.; Basche, T.; Wachtveitl, J. Acceptor Concentration Dependence of Förster Resonance Energy Transfer Dynamics in Dye– Quantum Dot Complexes. J. Phys. Chem. C 2014, 118, 4396-4402.
[11] Kilin, D. S.; Tsemekhman, K.; Prezhdo, O. V.; Zenkevich, E. I.; v. Borczykowski, C. Ab Initio Study of Exciton Transfer Dynamics from a Core-Shell Semiconductor Quantum Dot to a Porphyrine–Sensitizer. J. Photochem. Photobio. A 2007, 190, 342-351.
[12] Curutchet, C.; Franceschetti, A.; Zunger, A.; Scholes, G. D. Examining Förster Energy Transfer for Semiconductor Nanocrystalline Quantum Dot Donors and Acceptors. J. Phys. Chem. C 2008, 112, 1333613341.11
[13] Tamura, H.; Mallet, J.-M.; Oheim, M.; Burghardt, I. Ab Initio Study of Excitation Energy Transfer between Quantum Dots and Dye Molecules. J. Phys. Chem. C 2009, 113, 7548-7552.
[14] Lin, Z.; Franceschetti, A.; Lusk, M. T. Efficient Exciton Transport between Strongly Quantum–Confined Silicon Quantum Dots. ACSNano 2012, 6, 4029-4038.
[15] Verdenhalven, E.; Knorr, A.; Richter, M.; Bieniek, B.; Rinke, P. Theory of optical excitations in dipole-coupled hybrid molecule-semiconductor layers: Coupling of a molecular resonance to semiconductor continuum states. Phys. Rev. B 2014, 89, 235314.
[16] Specht, J.; Verdenhalven, E.; Bieniek, B.; Rinke, P.; Knorr, A.; Richter, M. Theory of excitation transfer between two-dimensional semiconductor and molecular layers. Phys. Rev. App. 2018, 9, 044025.
[17] Ziemann, D.; May, V. Distant and Shape-Dependent Excitation Energy Transfer in a Nanohybrid System: Computations on a Phephorbide-a CdSe Nanocrystal Complex. J. Chem. Phys. Lett. 2014, 5, 1203-1209.
[18] Plehn, Th.; Ziemann, D.; Megow, J.; May, V. Frenkel to Wannier-Mott Exciton Transition: Theory of FRET-Rates for a Tubular Dye Aggregate Coupled to a CdSe Nanocrystal. J. Chem. Phys. B 2015, 119, 7467-7472, John R. Miller and Marshall D. Newton Festschrift.
[19] Plehn, Th.; Ziemann, D.; May, V. Atomistic Simulations of Frenkel-Exciton to Wannier-Mott-Exciton Transitions in an Organic/Inorganic Nano-Hybrid System J. Chem. Phys. C 2018, 122, 27925-27934.
[20] Madjet, M. E.; Abdurahman, A.; Renger, T. Intermolecular Coulomb Couplings from Ab Initio Electrostatic Potentials: Application to Optical Transitions of Strongly Coupled Pigments in Photosynthetic Antennae and Reaction Centers. J. Phys. Chem. B 2006, 110, 17268-17281.
[21] Zhu, H.; May, V.; and Röder, B. Mixed Quantum Classical Simulations of Electronic Excitation Energy Transfer: The Pheophorbide-a DAB Dendrimer P4 in Solution. Chem. Phys. 2008, 351, 117-128.
[22] Megow, J.; Röhr, M.; Schmidt am Busch, M.; Renger, T.; Mitric, R.; Kirstein, S.; Rabe, J. P.; and May, V. Site-Dependence of van der Waals Interaction Explains Exciton Spectra of Double-Walled Tubular J-Aggregates. Phys. Chem. Chem. Phys. 2015, 17, 6741, arXiv:1412.3554 arXiv.org e-Print archive. http://arxiv.org/abs/1412.3554 (accessed Dec 11, 2014).
[23] Megow, J.; Körzdörfer, T.; Renger, T.; Sparenberg, M.; Blumstengel, S.; Henneberger, F.; May, V. Calculating Optical Absorption Spectra of Thin Polycrystalline Films: Structural Disorder and Site-Dependent van der Waals Interaction. 2014, arXiv:1411.2818 arXiv.org e-Print archive. http://xxx.tau.ac.il/abs/1411.2818 (accessed Nov 11, 2014).
[24] Wang, L.-W.; Zunger, A. Pseudopotential Calculations of Nanoscale CdSe Quantum Dots. Phys. Rev. B 1996, 53, 9579.
[25] Franceschetti, A.; Fu, H.; Wang, L. W.; Zunger, A. Many-Body Pseudopotential Theory of Excitons in InP and CdSe Quantum Dots. Phys. Rev. B 1999, 60, 1819.
[26] Schulz, S.; Schumacher, S.; Czycholl, G. Tight-Binding Model for Semiconductor Quantum Dots with a Wurtzite Crystal Structure: From One-Particle Properties to Coulomb Correlations and Optical Spectra. Phys. Rev. B 2006, 73, 245327.
[27] Baer, N.; Schulz, S.; Gartner, P.; Schuhmacher S.; Czycholl, G.; Jahnke, F. Influence of Symmetry and Coulomb Correlation Effects on the Optical Properties of Nitride Quantum Dots. Phys. Rev. B 2007, 76, 075310.
[28] Korkusinski, M.; Zielinski, M.; Hawrylak, P. Multiexciton Complexes in InAs Self- Assembled Quantum Dots. J. Appl. Phys. 2009, 105, 122406.
[29] Korkusinski, M.; Voznyy, O.; Hawrylak, P. Fine Structure and Size Dependence of Exciton and Bi-Exciton Optical Spectra in CdSe Nanocrystals. Phys. Rev. B 2010, 82, 245304.
[30] Megow, J.; Kulesza, A.; Qu,Z.–W.; Ronneberg, T.; Bonacic-Koutecky, V.; May, V. A Harmonic Approximation of Intramolecular Vibrations in a Mixed QuantumClassical Methodology: Linear Absorbance of a Dissolved Pheophorbid-a molecule as an Example Chem. Phys. 2010, 377, 10-14. 365-378.
[31] Eisele, D. M.; Cone, C. W.; Bloemsma, E. A.; Vlaming, S. M.; van der Kwaak, C. G. F.; Silbey, R. J.; Bawendi, M. G.; Knoester, J.; Rabe, J. P.; Vanden Bout, D. A. Utilizing Redox-Chemistry to Elucidate the Nature of Exciton Transitions in Supramolecular Dye Nanotubes. Nat. Chem. 2012, 4, 655-662.
[32] Deinert, J.-C.; Wegkamp, D.; Meyer, M.; Richter, C.; Wolf, M.; Stähler, J. Ultrafast Exciton Formation at the ZnO(10_10) Surface. Phys. Rev. Lett. 2014, 113, 057602.
[33] Friede, S.; Kuehn, S.; Sadovef, S.; Blumstengel, S.; Henneberger, F.; Elsaesser, Th.; Nanoscale Transport of Surface Excitons at the Interface between ZnO and a Molecular Layer. Phys. Rev. B 2015, 91, 121415(R).
[34] Resel, R. Crystallographic Studies on Hexaphenyl Thin Films - A Review. Thin Solid Films 2003, 433, 1-11.
[35] Blumstengel, S.; Glowatzki, H.; Sadofev, S.; Koch, N.; Kowarik, S.; Rabe, J. P.; Henneberger, F. Band-Offset Engineering in Organic/Inorganic Semiconductor Hybrid Structures. Phys. Chem. Chem. Phys. 2010, 12, 11642-11646.
[36] Sparenberg, M.; Zykov, A.; Beyer, P.; Pithan, L.; Weber, C.; Garmshausen, Y.; Carl ´ a, F.; Hecht, S.; Blumstengel, S.; Henneberger, F.; Kowarik, S. Controlling the Growth Mode of para-sexiphenyl (6P) on ZnO by Partial Fluorination. Phys. Chem. Chem. Phys. 2014, 16, 26084-26093.
[37] Plehn, Th.; May, V. Charge and Energy Migration in Molecular Clusters: A Stochastic Schroedinger Equation Approach. J. Chem. Phys. 2017, 146, 034107.
[38] Zojer, E.; Koch, N.; Puschnig, P.; Meghdadi, F.; Niko, A.; Resel, R.; Ambrosch- Draxl, C.; Knupfer, M.; Fink, J.; Bredas, J. L.; Leising, G. Structure, Morphology, and Optical Properties of Highly Ordered Films of para-sexiphenyl. Phys. Rev. B 2000, 61, 16538.
[39] Plehn, Th.; Ziemann, D.; May, V. Atomistic Simulations of Charge Separation at a Nano-Hybrid Interface: Relevance of Photoinduced Initial State Preparation. J. Phys. Chem. Lett. 2018, 9, 209.
[40] Plehn, Th.; Ziemann, D.; May, V. Charge Separation at an Organic/Inorganic Nano-Hybrid Interface: Atomistic Simulations of a Para-Sexiphenyl ZnO System Phys. Chem. Chem. Phys. 2018, 20, 26870.
[41] G. Kyas, Y. Zelinskyy, Y. Zhang and V. May, Theory of Metal Nano-Particle Affected Optical and Transport Properties in Supramolecular Complexes, in S. Haacke and I. Burghardt (eds.) ”Ultrafast Biomolecular Dynamics at the Nanoscale” Pan Stanford Publishing, Singapore, 2016.